
【题目】点![]() 为正方形
为正方形![]() 的边
的边![]() 上任意一点,在正方形内部做等腰直角
上任意一点,在正方形内部做等腰直角![]() .
.


(1)如图1,若![]() ,则
,则![]() _________(请直接写出答案)
_________(请直接写出答案)
(2)作![]() 关于
关于![]() 的对称点
的对称点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
①补全图形1;
②证明:四边形ECHF为平行四边形.
(3)在(2)的条件下,连接![]() ,请直接写出
,请直接写出![]() 和
和![]() 之间的数量关系.
之间的数量关系.
【答案】(1)![]() ;(2)①见解析;②见解析;(3)
;(2)①见解析;②见解析;(3)![]()
【解析】
(1)在![]() 中,利用勾股定理求得
中,利用勾股定理求得![]() ,再在是等腰直角三角形AEF中利用勾股定理即可求解;
,再在是等腰直角三角形AEF中利用勾股定理即可求解;
(2)①按照要求补全图形即可;
②作MN⊥AB,交DC于N,交AB于M,证得△AMF≌△FNE,根据全等三角形的性质证明点F在正方形ABCD的线BD上,设法证明FH=EC,FH∥EC,从而证明结论;
(3)根据②的过程,利用勾股定理证得 ![]() ,
,![]() ,从而得到
,从而得到![]() .
.
(1)∵四边形ABCD是正方形,AB=6,EC=2,
∴AB=AD=DC=6,∠ADE=90![]() ,
,
在![]() 中,AD= 6,DE=DC-EC=6-2=4,
中,AD= 6,DE=DC-EC=6-2=4,
∴![]() ,
,
∵![]() AEF是等腰直角三角形,且∠AFE=90
AEF是等腰直角三角形,且∠AFE=90![]() ,
,
∴AF=EF,
∵![]() ,即
,即![]() ,
,
∴![]() ;
;
(2)①补全图形如图所示:

②如图,过点F作MN⊥AB,交DC于N,交AB于M,连接BD,

∵AB∥CD,MN⊥AB,∠AFE=90![]() ,
,
∴MN⊥CD,
∴∠AFM+∠EFN=90°,∠AFM +∠FAM=90°,
∴∠EFN =∠FAM,
在△AMF和△FNE中,
 ,
,
∴△AMF≌△FNE(AAS),
∴AM=FN,MF=EN,
∵四边形ABCD是正方形,且MN⊥AB,
∴∠BAD=∠ADC=∠AMN=90°,
∴四边形ADNM是矩形,
∴AM=DN,
∴FN=DN,
又MN⊥CD,
∴∠FDN=45°,
∴点F在正方形ABCD的线BD上,
又F、H关于BC对称,
∴MF=FP=PH=EN,FP⊥BC,
∴四边形BPFM是正方形,四边形PCNF是矩形,
∴FP=NC,PC=FN,
∴FH=EC,
∵F、H关于BC对称,
∴FH⊥BC,
∵DC⊥BC,
∴FH∥EC,
∴四边形ECHF为平行四边形;
(3)由②得MF=FP,
∴![]() ,
,
∵AM=DN=FN,
∴![]() ,
,
∴![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图![]() ,已知
,已知![]() ,
,![]() 在
在![]() 的右倒,
的右倒,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() 所在直线交于点
所在直线交于点![]() ,
,![]() .
.
(1)求![]() 的度数.
的度数.
(2)若![]() ,求
,求![]() 的度数(用含
的度数(用含![]() 的代数式表示).
的代数式表示).
(3)将线段![]() 沿
沿![]() 方向平移,使得点
方向平移,使得点![]() 在点
在点![]() 的右侧,其他条件不变,在图
的右侧,其他条件不变,在图![]() 中画出平移后的图形,并判断
中画出平移后的图形,并判断![]() 的度数是否发生改变?若改变,求出它的度数(用含
的度数是否发生改变?若改变,求出它的度数(用含![]() 的式子表示);若不改变,请说明理由.
的式子表示);若不改变,请说明理由.


图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,且∠BAC=70°,AD是△ABC的角平分线,点E是AC边上的一点,点F为直线AB上的一动点,连结EF,直线EF与直线AD交于点P,设∠AEF=α°
(1)如图①,若 DE//AB,则①∠ADE的度数是_______;
②当∠DPE=∠DEP时,∠AEF= _____度:当∠PDE=∠PED,∠AEF=_______度;
(2)如图②,若DE⊥AC,则是否存在这样的α的值,使得△DPE中有两个相等的角?若存在求出α的值;若不存在,说明理由
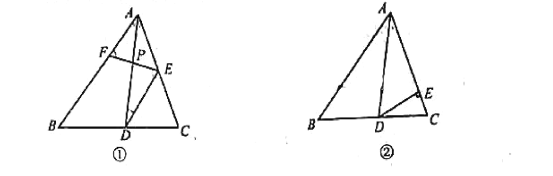
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水蜜桃是无锡市阳山的特色水果,水蜜桃一上市,水果店的老板用2000元购进一批水密桃,很快售完;老板又用3300元购进第二批水蜜桃,所购件数是第一批的![]() 倍,但进价比第一批每件多了5元.
倍,但进价比第一批每件多了5元.
(1)第一批水蜜桃每件进价是多少元?
(2)老板以每件65元的价格销售第二批水蜜桃,售出80%后,为了尽快售完,剩下的决定打折促销.要使得第二批水密桃的销售利润不少于288元,剩余的仙桃每件售价最多打几折?(利润=售价-进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+1经过点(2,6),且与直线y=![]() x+1相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).
x+1相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).

(1)求抛物线的解析式;
(2)若P是直线AB上方该抛物线上的一个动点,过点P作PD⊥x轴于点D,交AB于点E,求线段PE的最大值;
(3)在(2)的条件,设PC与AB相交于点Q,当线段PC与BE相互平分时,请求出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两块等腰直角三角形纸片AOB和COD按图1所示放置,直角顶点重合在点O处,AB=25,CD=17.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°)角度,如图2所示.
(1)利用图2证明AC=BD且AC⊥BD;
(2)当BD与CD在同一直线上(如图3)时,求AC的长和α的正弦值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题9分)把代数式通过配凑等手段,得到完全平方式,再运用完全平方式是非负性这一性质增加问题的条件,这种解题方法叫做配方法.配方法在代数式求值,解方程,最值问题等都有着广泛的应用.
例如:①用配方法因式分解:a2+6a+8
原式=a2+6a+9-1
=(a+3)2 –1
=(a+3-1)(a+3+1)
=(a+2)(a+4)
②若M=a2-2ab+2b2-2b+2,利用配方法求M的最小值:
a2-2ab+2b2-2b+2=a2-2ab+b2+b2-2b+1+1
=(a-b)2+(b-1)2 +1
∵(a-b)2≥0,(b-1)2 ≥0
∴当a=b=1时,M有最小值1
请根据上述材料解决下列问题:
(1)在横线上添上一个常数项使之成为完全平方式:a 2+4a+ .
(2)用配方法因式分解: a2-24a+143
(3)若M=![]() a2+2a +1,求M的最小值.
a2+2a +1,求M的最小值.
(4)已知a2+b2+c2-ab-3b-4c+7=0,求a+b+c的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com