
【题目】如果方程x2+px+q=0的两个根是x1 , x2 , 那么x1+x2=﹣p,x1x2=q,请根据以上结论,解决下列问题:
(1)已知关于x的方程x2+mx+n=0,(n≠0),求出一个一元二次方程,使它的两个根分别是已知方程两根的倒数;
(2)已知a、b满足a2﹣15a﹣5=0,b2﹣15b﹣5=0,求 ![]() 的值;
的值;
(3)已知a、b、c满足a+b+c=0,abc=16,求正数c的最小值.
【答案】
(1)解:设方程x2+mx+n=0,(n≠0)的两个根分别是x1,x2,
则: ![]() +
+ ![]() =
= ![]() =﹣
=﹣ ![]() ,
,
![]()
![]() =
= ![]() =
= ![]() ,
,
若一个一元二次方程的两个根分别是已知方程两根的倒数,
则这个一元二次方程是:x2+ ![]() x+
x+ ![]() =0
=0
(2)解:∵a、b满足a2﹣15a﹣5=0,b2﹣15b﹣5=0,
∴a,b是x2﹣15x﹣5=0的解,
当a≠b时,a+b=15,ab=﹣5,
![]() =
= ![]() =
= ![]() =
= ![]() =﹣47.
=﹣47.
当a=b时,原式=2
(3)解:∵a+b+c=0,abc=16,
∴a+b=﹣c,ab= ![]() ,
,
∴a、b是方程x2+cx+ ![]() =0的解,
=0的解,
∴c2﹣4 ![]() ≥0,
≥0,
c2﹣ ![]() ≥0,
≥0,
∵c是正数,
∴c3﹣43≥0,
c3≥43,
c≥4,
∴正数c的最小值是4
【解析】(1)先设方程x2+mx+n=0,(n≠0)的两个根分别是x1 , x2 , 得出 ![]() +
+ ![]() =﹣
=﹣ ![]() ,
, ![]()
![]() =
= ![]() ,再根据这个一元二次方程的两个根分别是已知方程两根的倒数,即可求出答案.(2)根据a、b满足a2﹣15a﹣5=0,b2﹣15b﹣5=0,得出a,b是x2﹣15x﹣5=0的解,求出a+b和ab的值,即可求出
,再根据这个一元二次方程的两个根分别是已知方程两根的倒数,即可求出答案.(2)根据a、b满足a2﹣15a﹣5=0,b2﹣15b﹣5=0,得出a,b是x2﹣15x﹣5=0的解,求出a+b和ab的值,即可求出 ![]() 的值.(3)根据a+b+c=0,abc=16,得出a+b=﹣c,ab=
的值.(3)根据a+b+c=0,abc=16,得出a+b=﹣c,ab= ![]() ,a、b是方程x2+cx+
,a、b是方程x2+cx+ ![]() =0的解,再根据c2﹣4
=0的解,再根据c2﹣4 ![]() ≥0,即可求出c的最小值.
≥0,即可求出c的最小值.
【考点精析】解答此题的关键在于理解求根公式的相关知识,掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根,以及对根与系数的关系的理解,了解一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=78°,则∠C的度数为=___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,A′、B′、C′分别为EF、EG、GF的中点,△A′B′C′的周长为_________.如果△ABC、△EFG、△A′B′C′分别为第1个、第2个、第3个三角形,按照上述方法继续作三角形,那么第n个三角形的周长是__________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
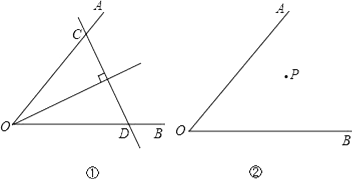
【题目】已知∠AOB及其内部一点P,试讨论以下问题的解答:
(1)如图①,若点P在∠AOB的平分线上,我们可以过P点作直线垂直于角平分线,分别交OA、OB于点C、D,则可以得到△OCD是以CD为底边的等腰三角形;若点P不在∠AOB的平分线上(如图②),你能过P点作直线,分别交OA、OB于点C、D,得到△OCD是等腰三角形,且CD是底边吗?请你在图②中画出图形,并简要说明画法.
(2)若点P不在∠AOB的平分线上(如图③),我们可以过P点作PQ∥OA,并作∠QPR=∠AOB,直线PR分别交OA、OB于点C、D,则可以得到△OCD是以OC为底的等腰三角形.请你说明这样作的理由.
(3)若点P不在∠AOB的平分线上,请你利用在(2)中学到的方法,在图④中过P点作直线分别交OA、OB于点C、D,使得△OCD是等腰三角形,且OD是底边.保留画图的痕迹,不用写出画法.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一根40cm的金属棒,欲将其截成x根7cm的小段和y根9cm的小段,剩余部分作废料处理,若使废料最少,则正整数x,y应分别为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,D是BC延长线上一点,E是BD垂直平分线与AB的交点,DE交AC于点F.求证:点E在AF的垂直平分线上.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com