
【题目】已知∠AOB及其内部一点P,试讨论以下问题的解答:
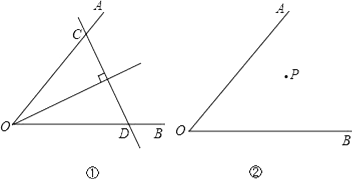
(1)如图①,若点P在∠AOB的平分线上,我们可以过P点作直线垂直于角平分线,分别交OA、OB于点C、D,则可以得到△OCD是以CD为底边的等腰三角形;若点P不在∠AOB的平分线上(如图②),你能过P点作直线,分别交OA、OB于点C、D,得到△OCD是等腰三角形,且CD是底边吗?请你在图②中画出图形,并简要说明画法.
(2)若点P不在∠AOB的平分线上(如图③),我们可以过P点作PQ∥OA,并作∠QPR=∠AOB,直线PR分别交OA、OB于点C、D,则可以得到△OCD是以OC为底的等腰三角形.请你说明这样作的理由.
(3)若点P不在∠AOB的平分线上,请你利用在(2)中学到的方法,在图④中过P点作直线分别交OA、OB于点C、D,使得△OCD是等腰三角形,且OD是底边.保留画图的痕迹,不用写出画法.

【答案】(1)能,画法见解析;(2)理由见解析;(3)见解析.
【解析】试题分析:(1)作∠AOB的平分线,过P点作角平分线的垂线,分别交角的两边OA、OB于点C、D,则△OCD是以CD为底边的等腰三角形;
(2)根据PQ∥OA,得出∠QPR=∠OCD,进而得出OD=CD,即可得出答案;
(3)作QP∥DO,再作∠ODR=∠O,即可得出答案.
试题解析:解:(1)能.
画法:作∠AOB的平分线,过P点作角平分线的垂线,分别交角的两边OA、OB于点C、D,则△OCD是以CD为底边的等腰三角形,如图①.
(2)∵PQ∥OA,∴∠QPR=∠OCD.
又∵∠QPR=∠AOB,∴∠OCD=∠AOB,∴OD=CD.
即△OCD是以OC为底的等腰三角形.
(3)如图②.
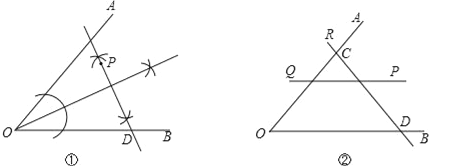


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
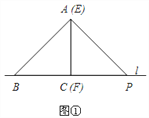
【题目】如图①,将两块全等的三角板拼在一起,其中△ABC的边BC在直线l上,AC⊥BC且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,EF⊥FP且EF=FP.
(1)在图①中,通过观察、测量,猜想直接写出AB与AP满足的数量关系和位置关系,不要说明理由;
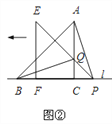
(2)将三角板△EFP沿直线l向左平移到图②的位置时,EP交AC于点Q,连接AP、BQ.猜想写出BQ与AP满足的数量关系和位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果方程x2+px+q=0的两个根是x1 , x2 , 那么x1+x2=﹣p,x1x2=q,请根据以上结论,解决下列问题:
(1)已知关于x的方程x2+mx+n=0,(n≠0),求出一个一元二次方程,使它的两个根分别是已知方程两根的倒数;
(2)已知a、b满足a2﹣15a﹣5=0,b2﹣15b﹣5=0,求 ![]() 的值;
的值;
(3)已知a、b、c满足a+b+c=0,abc=16,求正数c的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图1所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.
(1)填空:∠BAN=_____°;
(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
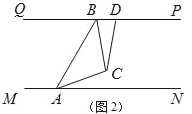
(3)如图2,若两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作∠ACD交PQ于点D,且∠ACD=120°,则在转动过程中,请探究∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某镇水库的可用水量为12000万m3,假设年降水量不变,能维持该镇16万人20年的用水量.为实施城镇化建设,新迁入了4万人后,水库只能够维持居民15年的用水量.
(1)问:年降水量为多少万m3?每人年平均用水量多少m3?
(2)政府号召节约用水,希望将水库的使用年限提高到25年.则该镇居民人均每年需节约多少m3水才能实现目标?
(3)某企业投入1000万元设备,每天能淡化5000m3海水,淡化率为70%.每淡化1m3海水所需的费用为1.5元,政府补贴0.3元.企业将淡化水以3.2元/m3的价格出售,每年还需各项支出40万元.按每年实际生产300天计算,该企业至少几年后能收回成本(结果精确到个位)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有以下说法:其中正确的说法有( )
(1)开方开不尽的数是无理数;
(2)无理数是无限循环小数
(3)无理数包括正无理数和负无理数;
(4)无理数都可以用数轴上的点来表示;
(5)循环小数都是有理数
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com