
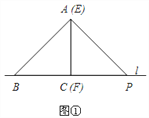
【题目】如图①,将两块全等的三角板拼在一起,其中△ABC的边BC在直线l上,AC⊥BC且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,EF⊥FP且EF=FP.
(1)在图①中,通过观察、测量,猜想直接写出AB与AP满足的数量关系和位置关系,不要说明理由;
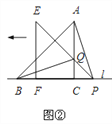
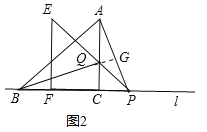
(2)将三角板△EFP沿直线l向左平移到图②的位置时,EP交AC于点Q,连接AP、BQ.猜想写出BQ与AP满足的数量关系和位置关系,并说明理由.
【答案】(1)AB=AP且AB⊥AP,(2)BQ与AP所满足的数量关系是AP=BQ,位置关系是AP⊥BQ
【解析】分析:(1)根据等腰直角三角形性质得出AB=AP,∠BAC=∠PAC=45°,求出∠BAP=90°即可;
(2)求出CQ=CP,根据SAS证△BCQ≌△ACP,推出AP=BQ,∠CBQ=∠PAC,根据三角形内角和定理求出∠CBQ+∠BQC=90°,推出∠PAC+∠AQG=90°,求出∠AGQ=90°即可.
详解:(1)AB=AP且AB⊥AP。理由如下:
∵AC⊥BC且AC=BC,∴△ABC为等腰直角三角形,
∴∠BAC=∠ABC=![]() (180°﹣∠ACB)=45°.
(180°﹣∠ACB)=45°.
又∵△ABC与△EFP全等,同理可证∠PEF=45°,
∴∠BAP=45°+45°=90°,∴AB=AP且AB⊥AP.
(2)BQ与AP所满足的数量关系是AP=BQ,位置关系是AP⊥BQ,理由如下:
延长BQ交AP于G,由(1)知,∠EPF=45°,∠ACP=90°,
∴∠PQC=45°=∠QPC,∴CQ=CP.
∵∠ACB=∠ACP=90°,AC=BC,∴在△BCQ和△ACP中,
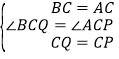 ,
,
∴△BCQ≌△ACP(SAS),
∴AP=BQ,∠CBQ=∠PAC.
∵∠ACB=90°,∴∠CBQ+∠BQC=90°.
∵∠CQB=∠AQG,∴∠AQG+∠PAC=90°,
∴∠AGQ=180°﹣90°=90°,∴AP⊥BQ.


科目:初中数学 来源: 题型:
【题目】(10分)如图所示,某公路一侧有A、B两个送奶站,C为公路上一供奶站,CA和CB为供奶路线,现已测得AC=8km,BC=15km,AB=17km,∠1=30°,若有一人从C处出发,沿公路边向右行走,速度为2.5km/h,问:多长时间后这个人距B送奶站最近?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,3)、B(﹣4,0).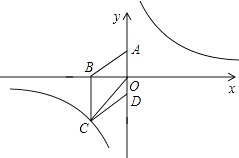
(1)求经过点C的反比例函数的解析式;
(2)设P是(1)中所求函数图象上一点,以P、O、A顶点的三角形的面积与△COD的面积相等.求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,A′、B′、C′分别为EF、EG、GF的中点,△A′B′C′的周长为_________.如果△ABC、△EFG、△A′B′C′分别为第1个、第2个、第3个三角形,按照上述方法继续作三角形,那么第n个三角形的周长是__________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
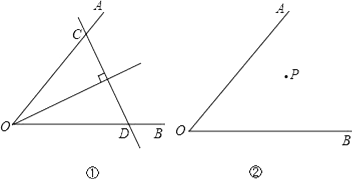
【题目】已知∠AOB及其内部一点P,试讨论以下问题的解答:
(1)如图①,若点P在∠AOB的平分线上,我们可以过P点作直线垂直于角平分线,分别交OA、OB于点C、D,则可以得到△OCD是以CD为底边的等腰三角形;若点P不在∠AOB的平分线上(如图②),你能过P点作直线,分别交OA、OB于点C、D,得到△OCD是等腰三角形,且CD是底边吗?请你在图②中画出图形,并简要说明画法.
(2)若点P不在∠AOB的平分线上(如图③),我们可以过P点作PQ∥OA,并作∠QPR=∠AOB,直线PR分别交OA、OB于点C、D,则可以得到△OCD是以OC为底的等腰三角形.请你说明这样作的理由.
(3)若点P不在∠AOB的平分线上,请你利用在(2)中学到的方法,在图④中过P点作直线分别交OA、OB于点C、D,使得△OCD是等腰三角形,且OD是底边.保留画图的痕迹,不用写出画法.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有七张正面分别标有数字﹣3,﹣2,﹣1,0,1,2,3的卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为a,则使关于x的一元二次方程x2﹣2(a﹣1)x+a(a﹣3)=0有两个不相等的实数根,且以x为自变量的二次函数y=x2﹣(a2+1)x﹣a+2的图象不经过点(1,O)的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com