
【题目】如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,3)、B(﹣4,0).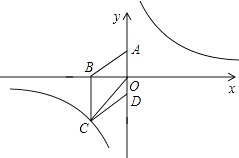
(1)求经过点C的反比例函数的解析式;
(2)设P是(1)中所求函数图象上一点,以P、O、A顶点的三角形的面积与△COD的面积相等.求点P的坐标.
【答案】
(1)
解:由题意知,OA=3,OB=4
在Rt△AOB中,AB= ![]()
∵四边形ABCD为菱形
∴AD=BC=AB=5,
∴C(﹣4,﹣5).
设经过点C的反比例函数的解析式为 ![]() (k≠0),
(k≠0),
则 ![]() =﹣5,解得k=20.
=﹣5,解得k=20.
故所求的反比例函数的解析式为 ![]()
(2)
解:设P(x,y)
∵AD=AB=5,OA=3,
∴OD=2,S△COD= ![]()
即 ![]() ,
,
∴|x|= ![]() ,
,
∴ ![]()
当x= ![]() 时,y=
时,y= ![]() =
= ![]() ,当x=﹣
,当x=﹣ ![]() 时,y=
时,y= ![]() =﹣
=﹣ ![]()
∴P( ![]() )或(
)或( ![]() )
)
【解析】(1)根据菱形的性质可得菱形的边长,进而可得点C的坐标,代入反比例函数解析式可得所求的解析式;(2)设出点P的坐标,易得△COD的面积,利用点P的横坐标表示出△PAO的面积,那么可得点P的横坐标,就求得了点P的坐标.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,E、F、G、H依次是各边中点,O是四边形ABCD内一点, 若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为7、9、10,则四边形DHOG的面积为( )

A. 7 B. 8 C. 9 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某产品的标志图案如图(1)所示,要在所给的图3-122(2)中,把A,B,C三个菱形通过一种或几种变换,使之变为与图(1)一样的图案.
(1)请你在图3-122(2)中作出变换后的图案;(最终图案用实线)
(2)你所用的变换方法是_________.(填序号)
①将菱形B向上平移;②将菱形B绕点O顺时针旋转120°;③将菱形B绕点O旋转180.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE、始终经过点A,EF与AC交于M点. 
(1)求证:△ABE∽△ECM;
(2)探究:在△DEF运动过程中,重叠部分能否构成等腰三角形?若能,求出BE的长;若不能,请说明理由;
(3)当线段AM最短时,求重叠部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
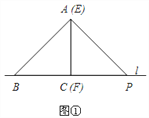
【题目】如图①,将两块全等的三角板拼在一起,其中△ABC的边BC在直线l上,AC⊥BC且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,EF⊥FP且EF=FP.
(1)在图①中,通过观察、测量,猜想直接写出AB与AP满足的数量关系和位置关系,不要说明理由;
(2)将三角板△EFP沿直线l向左平移到图②的位置时,EP交AC于点Q,连接AP、BQ.猜想写出BQ与AP满足的数量关系和位置关系,并说明理由.
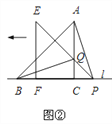
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com