
【题目】有一根40cm的金属棒,欲将其截成x根7cm的小段和y根9cm的小段,剩余部分作废料处理,若使废料最少,则正整数x,y应分别为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】分析:根据金属棒的长度是40cm即可得到关于x一元一次不等式,即7x+9y≤40,再根据x,y都是正整数,求得所有可能的结果,分别计算出废料的长度,再找出最少的费料对应的x、y值即可.
详解:根据题意得:7x+9y≤40,
则x≤![]() .
.
∵40-9y≥0且y是正整数,
∴y的值可以是1或2或3或4,
当y=1时,x≤![]() ,则x=4,此时所剩的废料是:40-1×9-4×7=3(cm);
,则x=4,此时所剩的废料是:40-1×9-4×7=3(cm);
当y=2时,x≤![]() ,则x=3,此时所剩的废料是:40-2×9-3×7=1(cm);
,则x=3,此时所剩的废料是:40-2×9-3×7=1(cm);
当y=3时,x≤![]() ,则x=1,此时所剩的废料是:40-3×9-7=6(cm);
,则x=1,此时所剩的废料是:40-3×9-7=6(cm);
当y=4时,x≤![]() ,则x=0(舍去).
,则x=0(舍去).
综上所述,当废料最少时,x=3,y=2.


科目:初中数学 来源: 题型:
【题目】如果方程x2+px+q=0的两个根是x1 , x2 , 那么x1+x2=﹣p,x1x2=q,请根据以上结论,解决下列问题:
(1)已知关于x的方程x2+mx+n=0,(n≠0),求出一个一元二次方程,使它的两个根分别是已知方程两根的倒数;
(2)已知a、b满足a2﹣15a﹣5=0,b2﹣15b﹣5=0,求 ![]() 的值;
的值;
(3)已知a、b、c满足a+b+c=0,abc=16,求正数c的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某镇水库的可用水量为12000万m3,假设年降水量不变,能维持该镇16万人20年的用水量.为实施城镇化建设,新迁入了4万人后,水库只能够维持居民15年的用水量.
(1)问:年降水量为多少万m3?每人年平均用水量多少m3?
(2)政府号召节约用水,希望将水库的使用年限提高到25年.则该镇居民人均每年需节约多少m3水才能实现目标?
(3)某企业投入1000万元设备,每天能淡化5000m3海水,淡化率为70%.每淡化1m3海水所需的费用为1.5元,政府补贴0.3元.企业将淡化水以3.2元/m3的价格出售,每年还需各项支出40万元.按每年实际生产300天计算,该企业至少几年后能收回成本(结果精确到个位)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB分别切⊙O于A、B,连接PO、AB相交于D,C是⊙O上一点,∠C=60°. 
(1)求∠APB的大小;
(2)若PO=20cm,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有以下说法:其中正确的说法有( )
(1)开方开不尽的数是无理数;
(2)无理数是无限循环小数
(3)无理数包括正无理数和负无理数;
(4)无理数都可以用数轴上的点来表示;
(5)循环小数都是有理数
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF.
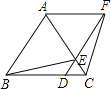
(1)请在图中找出一对全等三角形,用符号“≌”表示,并加以证明;
(2)判断四边形ABDF是怎样的四边形,并说明理由;
(3)若AB=6,BD=2DC,求四边形ABEF的面积..
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com