
【题目】如图,PA、PB分别切⊙O于A、B,连接PO、AB相交于D,C是⊙O上一点,∠C=60°. 
(1)求∠APB的大小;
(2)若PO=20cm,求△AOB的面积.
【答案】
(1)解:∵PA、PB分别切⊙O于A、B,
∴OA⊥PA,OB⊥PB,
∴∠PAO=∠PBO=90°,
∵∠C=60°,
∴∠AOB=2∠C=2×60°=120°,
∴∠APB=360°﹣∠PAO﹣∠PBO﹣∠AOB=60°
(2)解:∵PA、PB分别切⊙O于A、B,
∴∠PAO=∠PBO=90°,∠APO= ![]() ∠APB=
∠APB= ![]() ×60°=30°,PA=PB,
×60°=30°,PA=PB,
∴P在AB的垂直平分线上,
∵OA=OB,
∴O在AB的垂直平分线上,
即OP是AB的垂直平分线,
即OD⊥AB,AD=BD= ![]() AB,
AB,
∵∠PAO=90°,
∴∠AOP=60°,
在Rt△PAO中,AO= ![]() PO=
PO= ![]() ×20=10(cm),
×20=10(cm),
在Rt△AOD中,AD=AOsin60°=10× ![]() =5
=5 ![]() (cm),OD=OAcos60°=10×
(cm),OD=OAcos60°=10× ![]() =5(cm),
=5(cm),
∴AB=2AD=10 ![]() cm,
cm,
∴△AOB的面积为: ![]() ABOD=
ABOD= ![]() ×10
×10 ![]() ×5=25
×5=25 ![]() (cm2)
(cm2)
【解析】(1)由PA、PB分别切⊙O于A、B,由切线的性质,即可得OA⊥PA,OB⊥PB,又由圆周角定理,求得∠AOB的度数,继而求得∠APB的大小;(2)由切线长定理,可求得∠APO的度数,继而求得∠AOP的度数,易得PO是AB的垂直平分线,然后利用三角函数的性质,求得AD与OD的长,继而求得答案.
【考点精析】根据题目的已知条件,利用圆周角定理和切线的性质定理的相关知识可以得到问题的答案,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


科目:初中数学 来源: 题型:
【题目】如图,△ABC的中线BE,CF相交于点G,P、Q分别是BG、CG的中点.
(1)求证:四边形EFPQ是平行四边形;
(2)请直接写出BG与GE的数量关系.(不要求证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等腰直角△ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A:P′C=1:3,则P′A:PB=( ) 
A.1: ![]()
B.1:2
C.![]() :2
:2
D.1: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一根40cm的金属棒,欲将其截成x根7cm的小段和y根9cm的小段,剩余部分作废料处理,若使废料最少,则正整数x,y应分别为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图1,在四边形ABCD中,BC=AD,AB=

求证:四边形ABCD是 四边形.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇同学的思路写出证明过程;
(3)用文字叙述所证命题的逆命题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E、F分别是边AD、CD上的点,DE=CF,AF与BE相交于O,DG⊥AF,垂足为G. 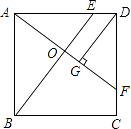
(1)求证:AF⊥BE;
(2)试探究线段AO、BO、GO的长度之间的数量关系;
(3)若GO:CF=4:5,试确定E点的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD内的一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,则∠BE′C=__度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com