
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AEF,延长EF交边BC于点G,连结AG,CF,则下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EGC=S△AFE;⑤S△FGC=![]() ;其中正确的结论有_____.
;其中正确的结论有_____.

【答案】①②③④⑤
【解析】
由正方形和折叠的性质得出AF=AB,∠B=∠AFG=90°,由HL即可证明Rt△ABG≌Rt△AFG,得出①正确,设BG=x,则CG=BC-BG=6-x,GE=GF+EF=BG+DE=x+2,由勾股定理求出x=3,得出②正确;由等腰三角形的性质和外角关系得出∠AGB=∠FCG,证出平行线,得出③正确;分别求出△EGC,△AEF的面积,可以判断④,由![]()
,可求出△FGC的面积,故此可对⑤做出判断.
解:解:∵四边形ABCD是正方形,
∴AB=AD=DC=6,∠B=D=90°,
∵CD=3DE,
∴DE=2,
∵△ADE沿AE折叠得到△AFE,
∴DE=EF=2,AD=AF,∠D=∠AFE=∠AFG=90°,
∴AF=AB,
∵在Rt△ABG和Rt△AFG中,
![]() ,
,
∴Rt△ABG≌Rt△AFG(HL).
∴①正确;
∵Rt△ABG≌Rt△AFG,
∴BG=FG,∠AGB=∠AGF.
设BG=x,则CG=BC-BG=6-x,GE=GF+EF=BG+DE=x+2.
在Rt△ECG中,由勾股定理得:CG2+CE2=EG2.
∵CG=6-x,CE=4,EG=x+2,
∴(6-x)2+42=(x+2)2,解得:x=3.
∴BG=GF=CG=3.
∴②正确;
∵CG=GF,
∴∠CFG=∠FCG.
∵∠BGF=∠CFG+∠FCG,∠BGF=∠AGB+∠AGF,
∴∠CFG+∠FCG=∠AGB+∠AGF.
∵∠AGB=∠AGF,∠CFG=∠FCG,
∴∠AGB=∠FCG.
∴AG∥CF.
∴③正确;
∵S△EGC=![]() ×3×4=6,S△AEF=S△ADE=
×3×4=6,S△AEF=S△ADE=![]() ×6×2=6,
×6×2=6,
∴S△EGC=S△AFE;
∴④正确,
∵△CFG和△CEG中,分别把FG和GE看作底边,
则这两个三角形的高相同.
∴![]() ,
,
∵S△GCE=6,
∴S△CFG=![]() ×6=3.6,
×6=3.6,
∴⑤正确;
故答案为①②③④⑤.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA=2,OB=3,现同时将点A,B分别向上平移2个单位,再向右平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD.
(1)求点C、D的坐标及四边形ABDC的面积;
(2)若点Q在线的CD上移动(不包括C,D两点).QO与线段AB,CD所成的角∠1与∠2如图所示,给出下列两个结论:①∠1+∠2的值不变;②![]() 的值不变,其中只有一个结论是正确的,请你找出这个结论,并求出这个值.
的值不变,其中只有一个结论是正确的,请你找出这个结论,并求出这个值.
(3)在y轴正半轴上是否存在点P,使得S△CDP=S△PBO?如果有,试求出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级2班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):

(l)甲队成绩的中位数是____分,乙队成绩的众数是____分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队的平均成绩是9分,方差是1.4分,则成绩较为整齐的是哪个队?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,直线
,直线![]() 分别与
分别与![]() 、
、![]() 交于点
交于点![]() 、点
、点![]() .
.
(1)如图1,当点![]() 在线段
在线段![]() 上,若
上,若![]() ,
,![]() ,则
,则![]() __________°;
__________°;

(2)如图2,当点![]() 在线段
在线段![]() 的延长线上,
的延长线上,![]() 与
与![]() 交于点
交于点![]() ,则
,则![]() 、
、![]() 、
、![]() 之间满足怎样的关系,请证明你的结论;
之间满足怎样的关系,请证明你的结论;

(3)如图3,在(2)的条件下,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,射线
,射线![]() 将
将![]() 分成
分成![]() ,且与
,且与![]() 交于点
交于点![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿对角线AC翻折,点B落在点E处,EC交AD于F.
(1)求证:△AEF≌△CDF;
(2)若AB=4,BC=8,EF=3,求图中阴影部分的面积。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1与直线l2:y=![]() x+3平行,直线l1与x轴的交点的坐标为A(2,0),求:
x+3平行,直线l1与x轴的交点的坐标为A(2,0),求:
(1)直线l1的表达式.
(2)直线l1与坐标轴围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
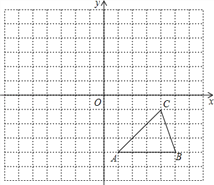
【题目】每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,
①写出A、B、C的坐标.
②以原点O为对称中心,画出△ABC关于原点O对称的△A1B1C1,并写出A1、B1、C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一副秋千架,左图是从正面看,当秋千绳子自然下垂时,踏板离地面0.5m(踏板厚度忽略不计), 右图是从侧面看,当秋千踏板荡起至点B位置时,点B离地面垂直高度BC为1m,离秋千支柱AD的水平距离BE为1.5m(不考虑支柱的直径).求秋千支柱AD的高.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:一次函数 ![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点 ![]() ,
,![]() .
.
(1)分别求出这两个函数的表达式;
(2)直接写出当一次函数的函数值大于反比例函数的函数值时,![]() 的取值范围为______.
的取值范围为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com