
【题目】如图,在平面直角坐标系中,OA=2,OB=3,现同时将点A,B分别向上平移2个单位,再向右平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD.
(1)求点C、D的坐标及四边形ABDC的面积;
(2)若点Q在线的CD上移动(不包括C,D两点).QO与线段AB,CD所成的角∠1与∠2如图所示,给出下列两个结论:①∠1+∠2的值不变;②![]() 的值不变,其中只有一个结论是正确的,请你找出这个结论,并求出这个值.
的值不变,其中只有一个结论是正确的,请你找出这个结论,并求出这个值.
(3)在y轴正半轴上是否存在点P,使得S△CDP=S△PBO?如果有,试求出点P的坐标.

【答案】(1)C(0,2)、D(5,2);S四边形ABDC=10;(2)∠1+∠2=180°;证明见解析;(3)存在,点P的坐标为(0,![]() )或(0,5).
)或(0,5).
【解析】
(1)依据平移与坐标变化的规律可求的点C、D的坐标,由点的坐标可求得AB、OC的长,从而可求得四边形ABDC的面积;
(2)依据平行的性质可证明∠1+∠2=180°;
(3)设点P的坐标(0,a),然后依据三角形的面积公式列方程求解即可.
(1)OA=2,OB=3,
∴A(﹣2,0)、B(3,0).
∵将点A,B分别向上平移2个单位,再向右平移2个单位,分别得到点A,B的对应点C,D,
∴C(0,2)、D(5,2).
∵由平移的性质可知:AB∥CD,AB=CD,
∴ABCD为平行四边形.
∴四边形ABDC的面积=ABOC=5×2=10.
(2)∠1+∠2=180°.
证明:如图1所示;

∵AB∥CD,
∴∠1=∠3.
∵∠3+∠2=180°.
∴∠1+∠2=180°.
∴∠1+∠2为定值.
∵∠1+∠2=180°,
∴∠2=180°﹣∠1.
∴![]() =
=![]() =
=![]() ﹣1.
﹣1.
∵当点Q在CD上运动时,∠1的度数在不断变化,
∴![]() ﹣1在不断变化,即
﹣1在不断变化,即![]() 的值在不断变化;
的值在不断变化;
(3)如图2所示:设点P的坐标为(0,a),则PC=(2﹣a),PO=a.

∵S△CDP=S△PBO,
∴![]() DCPC=
DCPC=![]() OBOP.
OBOP.
∴![]() ×5(2﹣a)=
×5(2﹣a)=![]() ×3×a.
×3×a.
∴10﹣5a=3a
解得:a=![]()
如图3所示:设点P的坐标为(0,a),则PC=a﹣2,PO=a.

∵S△CDP=S△PBO,
∴![]() DCPC=
DCPC=![]() OBOP.
OBOP.
∴![]() ×5×(a﹣2)=
×5×(a﹣2)=![]() ×3×a.
×3×a.
∴5a﹣10=3a.
解得:a=5.
综上所述,点P的坐标为(0,![]() )或(0,5).
)或(0,5).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”,根据图形,回答下列问题.
(1)图中格点三角形A′B′C′是由格点三角形ABC通过怎样的平移得到的?
(2)如果以直线a,b为坐标轴建立平面直角坐标系后,点A的坐标为(-3,4),请写出格点三角形DEF各顶点的坐标,并求出三角形DEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班从三名男生(含小强)和五名女生中选四名学生参加学校举行的“中华古诗文朗诵大赛”,规定女生选n名.
(1)当n为何值时,男生小强参加是确定事件?
(2)当n为何值时,男生小强参加是随机事件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校标准化建设需购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑和每台电子白板各多少万元;
(2)根据学校需要,实际购进电脑和电子白板共30台,总费用30万元,请你通过计算求学校购买了电脑和电子白板各多少台.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
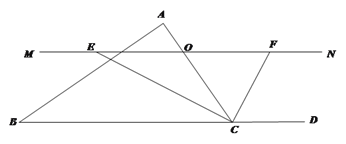
【题目】已知△ABC中,点O是边AC上的一个动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:OE=OF.
(2)试确定点O在边AC上的位置,使四边形AECF是矩形,并加以证明.
(3)在(2)的条件下,且△ABC满足 ____________时,矩形AECF是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划组织师生参加哈尔滨冰雪节,感受冰雪艺术的魅力.出租公司现有甲、乙两种型号的客车可供租用,且每辆乙型客车的租金比每辆甲型客车少60元.若该校租用3辆甲种客车,4辆乙种客车,则需付租金1720元.
(1)该出租公司每辆甲、乙两型客车的租金各为多少元?
(2)若学校计划租用6辆客车,租车的总租金不超过1560元,那么最多租用甲型客车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在菱形ABCD中,E,F分别是BC,CD上的点,且CE=CF

(1)求证:△ABE≌△ADF
(2)过点C作CG‖EA交AF于点H,交AD于点G,若∠BAE=25°,∠BCD=130°,求∠AHC
的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AEF,延长EF交边BC于点G,连结AG,CF,则下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EGC=S△AFE;⑤S△FGC=![]() ;其中正确的结论有_____.
;其中正确的结论有_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com