
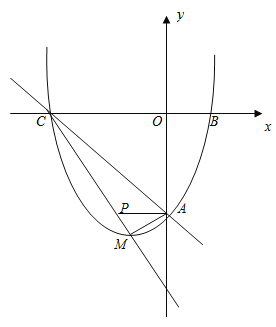
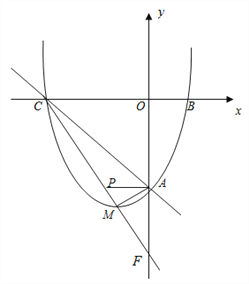
【题目】如图,已知抛物线y=ax2+bx+c与x轴交于点B,C,与直线AC:y=-x-6交y轴于点A,点M是抛物线的顶点,且横坐标为-2.
(1)求出抛物线的表达式.
(2)判断△ACM的形状并说明理由.
(3)直线CM交y轴于点F,在直线CM上是否存在一点P,使∠CMA=∠PAF,若存在,求出P的坐标,若不存在,说明理由.
【答案】(1)![]() ;(2)△ACM为直角三角形,理由见解析;(3)存在,
;(2)△ACM为直角三角形,理由见解析;(3)存在, ![]() ,
, ![]()
【解析】解:(1) A(0,-6) C(-6,0)
∴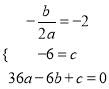
解得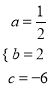
∴此抛物线的表达式为![]() .
.
(2)△ACM为直角三角形,理由如下:
M(-2,-8)
∴AC2+AM2=72+22+(8-6)2=80
MC2=42+82=80
∴AC2+AM2=MC2
∴△ACM为直角三角形
(3)假设存在
设直线CM的解析式为y=kx+b过C(-6,0)、M(-2,-8)则
![]()
解得![]()
∴y=-2x-12
设P(n,-2n-12)
∴∠CMA=∠MAF+∠AFM ∠PAF=∠MAF+∠PAM
又 ∠APF=∠MPA ∴ △APF~△MPA
∴![]() 即
即![]()
∴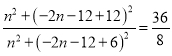
∴ 35n2+216n+324=0
∴![]() ,
, ![]()
∴ 符合条件的P点有两个,其坐标分别为 :
![]() ,
, ![]()


科目:初中数学 来源: 题型:
【题目】如果规定收入为正,支出为负,收入200元记作+200元,那么支出37元记作( )
A. 200元 B. -37元 C. 163元 D. 37元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD的面积为300cm2 , 长和宽的比为3:2.在此长方形内沿着边的方向能否并排裁出两个面积均为147cm2的圆(π取3),请通过计算说明理由. 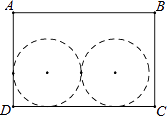
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角△ABC中,∠BAC=45°,AB=2,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣3x2y)2(6xy3)÷(9x3y4)
(2)(x﹣2y)(x+2y)﹣4y(x﹣y)
(3)( ![]() a+3b)2﹣(
a+3b)2﹣( ![]() a﹣3b)2
a﹣3b)2
(4)(﹣2)24(﹣0.125)8+20162﹣2015×2017.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1∥l2 , 且l4和l1、l2分别交于A、B两点,点P为线段AB上的一个定点如图1) 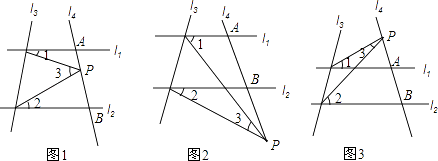
(1)写出∠1、∠2、∠3、之间的关系并说出理由.
(2)如果点P为线段AB上的动点时,问∠1、∠2、∠3之间的关系是否发生变化?(必说理由)
(3)如果点P在A、B两点外侧运动时,(点P和点A、点B不重合)
①如图2,当点P在射线AB上运动时,∠1、∠2、∠3之间关系并说出理由.
②如图3,当点P在射线BA上运动时,∠1、∠2、∠3之间关系(不说理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题9分)据报道,“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.某校学生会想知道学生对这个提议的了解程度,随机抽取部分学生进行了一次问卷调查,并根据收集到的信息进行了统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
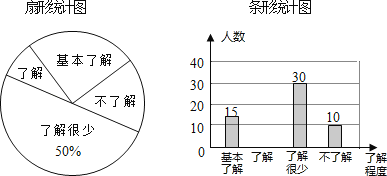
(1)接受问卷调查的学生共有___名,扇形统计图中“基本了解”部分所对应扇形的圆心角为___;请补全条形统计图;
(2)若该校共有学生900人,请根据上述调查结果,估计该校学生中对将“剪刀石头布”作为奥运会比赛项目的提议达到“了解”和“基本了解”程度的总人数;
(3)“剪刀石头布”比赛时双方每次任意出“剪刀”、“石头”、“布”这三种手势中的一种,规则为:剪刀胜布,布胜石头,石头胜剪刀,若双方出现相同手势,则算打平.若小刚和小明两人只比赛一局,请用树状图或列表法求两人打平的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com