
【题目】如图,在Rt△ACB中,∠C=90°,AC=30cm,BC=25cm,动点P从点C出发,沿CA方向运动,速度是2cm/s,动点Q从点B出发,沿BC方向运动,速度是1cm/s.
(1)几秒后P,Q两点相距25cm?
(2)几秒后△PCQ与△ABC相似?
(3)设△CPQ的面积为S1 , △ABC的面积为S2 , 在运动过程中是否存在某一时刻t,使得S1:S2=2:5?若存在,求出t的值;若不存在,则说明理由.
【答案】
(1)
解:设x秒后P、Q两点相距25cm,
则CP=2xcm,CQ=(25﹣x)cm,
由题意得,(2x)2+(25﹣x)2=252,
解得,x1=10,x2=0(舍去),
则10秒后P、Q两点相距25cm
(2)
解:设y秒后△PCQ与△ABC相似,
当△PCQ∽△ACB时, ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得,y= ![]() ,
,
当△PCQ∽△BCA时, ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得,y= ![]() ,
,
故 ![]() 秒或
秒或 ![]() 秒后△PCQ与△ABC相似
秒后△PCQ与△ABC相似
(3)
解:△CPQ的面积为S1= ![]() ×CQ×CP=
×CQ×CP= ![]() ×2t×(25﹣t)=﹣t2+25t,
×2t×(25﹣t)=﹣t2+25t,
△ABC的面积为S2= ![]() ×AC×BC=375,
×AC×BC=375,
由题意得,5(﹣t2+25t)=375×2,
解得,t1=10,t2=15,
故运动10秒或15秒时,S1:S2=2:5
【解析】(1)设x秒后P、Q两点相距25cm,用x表示出CP、CQ,根据勾股定理列出方程,解方程即可;(2)分△PCQ∽△ACB和△PCQ∽△BCA两种情况,根据相似三角形的性质列出关系式,解方程即可;(3)用t分别表示出CP、CQ,根据题意列出方程,解方程即可.


科目:初中数学 来源: 题型:
【题目】在四张背面完全相同的纸牌A、B、C、D中,其中正面分别画有四个不同的几何图形(如图),小华将这4张纸牌背面朝上洗匀后摸出一张(不放回),再从余下的3张纸牌中摸出一张.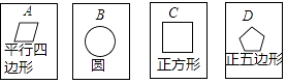
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出两张纸牌牌面上所画几何图形,既是轴对称图形又是中心对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB上有两点C、D,且AC=BD,M、N分别是线段AC 、AD的中点,若AB=a cm ,AC=BD=b cm,且a,b满足(a-9)2+|b-7 |=0.
![]()
(1)求AB ,AC的长度;
(2)求线段MN的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
如图①,在△ABC中,试说明∠A+∠B+∠C=180°.
分析:通过画平行线,将∠A、∠B、∠C作等量代换,使各角之和恰为一个平角,依辅助线不同而得多种方法.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB∥CD,∠ABE与∠CDE两个角的角平分线相交于点F.
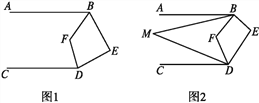
(1)如图1,若∠E=80°,求∠BFD的度数.
(2)如图2,若∠ABM=![]() ∠ABF,∠CDM=
∠ABF,∠CDM=![]() ∠CDF,试写出∠M与∠E之间的数量关系并证明你的结论.
∠CDF,试写出∠M与∠E之间的数量关系并证明你的结论.
(3)若∠ABM=![]() ∠ABF,∠CDM=
∠ABF,∠CDM=![]() ∠CDF,∠E=m°,请直接用含有n,m°的代数式表示出∠M.
∠CDF,∠E=m°,请直接用含有n,m°的代数式表示出∠M.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AE于点E. 
(1)求证:△BEF∽△DBC.;
(2)若⊙O的半径为3,∠C=32°,求BE的长.(精确到0.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE、BF、DC是直线,B在直线AC上,E在直线DF上,∠1=∠2,∠A=∠F.
求证:∠C=∠D.

证明:因为∠1=∠2(已知),∠1=∠3( )
得∠2=∠3( )
所以AE//_______( )
得∠4=∠F( )
因为__________(已知)
得∠4=∠A
所以______//_______( )
所以∠C=∠D( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com