
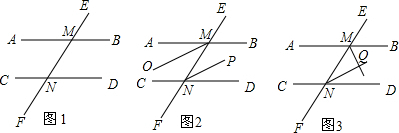
 解:(1)如图1,直线AB,CD被直线EF所截,且AB∥CD,根据 两直线平行,内错角相等可得∠AMN=∠DNM;
解:(1)如图1,直线AB,CD被直线EF所截,且AB∥CD,根据 两直线平行,内错角相等可得∠AMN=∠DNM;

 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
| 组别 | 分 组 | 频数 | 频率 |
| 1 | 89.5~99.5 | 4 | 0.04 |
| 2 | 99.5~109.5 | 3 | 0.03 |
| 3 | 109.5~119.5 | 46 | 0.46 |
| 4 | 119.5~129.5 | b | e |
| 5 | 129.5~139.5 | 6 | 0.06 |
| 6 | 139.5~149.5 | 2 | 0.02 |
| 合 计 | a | 1.00 | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com