练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，已知，分别是的高和中线，，，，，试求：

    (1)的长；

    (2)和的周长的差.

    【答案】(1)长为;(2)周长差.

    【解析】

    （1）利用直角三角形的面积法求线段AD的长度；
    （2）由于AE是中线，那么BE=CE，再表示△ACE的周长和△ABE的周长，化简可得△ACE的周长-△ABE的周长=AC-AB，即可求解．

    解：（1）∵∠BAC=90°，AD是边BC上的高，
    ∴S△ACB=ABAC=BCAD，
    ∵，，，
    ∴AD=8×15÷17= （cm），
    即AD的长度为cm；
    （2）∵AE为BC边上的中线，
    ∴BE=CE，
    ∴△ACE的周长-△ABE的周长=AC+AE+CE-（AB+BE+AE）=AC-AB=15-8=7（cm），
    即△ACE和△ABE的周长的差是7cm．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，五边形ABCDE中有一正三角形ACD，若AB=DE，BC=AE，∠E=115°，则∠BAE的度数为何？（　　）

    A. 115 B. 120 C. 125 D. 130

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在正方形ABCD中，对角线BD所在的直线上有两点E、F满足BE=DF，连接AE、AF、CE、CF，如图所示．

    （1）求证：△ABE≌△ADF；

    （2）试判断四边形AECF的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）如图1，计算下列五角星图案中五个顶角的度数和. 即：求∠A+∠B+∠C+∠D+∠E的大小.

    （2）如图2，若五角星的五个顶角的度数相等， 求∠1的大小.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】写出下列事件发生的可能性，并标在图中的大致位置上．

    (1)袋中有10个红球，摸到红球；

    (2)袋中有10个红球，摸到白球；

    (3)一副混合均匀的扑克牌(除去大、小王)，从中任意抽取一张，这一张恰好是A；

    (4)一个布袋中有2个黑球和2个白球，从中任意摸出一个球，恰好是黑球；

    (5)任意掷出一个质地均匀的骰子(每个面上分别标有数字1，2，3，4，5，6)，朝上一面的数字大于2.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小南发现操场中有一个不规则的封闭图形ABC．为了知道它的面积，他在封闭图形内画出了一个半径为1米的圆，在不远处向圈内掷石子，若石子落在图形ABC以外，则重掷．记录如下：

    石子落在圆内（含圆上）的次数

    14

    43

    93

    150

    石子落在阴影内的次数

    23

    91

    186

    300

    根据以上的数据，小南得到了封闭图形ABC的面积．

    请根据以上信息，回答以下问题：

    （1）求石子落在圆内（含圆上）的频率；

    （2）估计封闭图形ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）某校招聘教师一名，现有甲、乙、丙三人通过专业知识、讲课、答辩三项测试，他们各自的成绩如下表所示：

    应聘者

    专业知识

    讲课

    答辩

    甲

    70

    85

    80

    乙

    90

    85

    75

    丙

    80

    90

    85

    按照招聘简章要求，对专业知识、讲课、答辩三项赋权5：4：1．请计算三名应聘者的平均成绩，从成绩看，应该录取谁？

    （2）我市举行了某学科实验操作考试，有A、B、C、D四个实验，规定每位学生只参加其中一个实验的考试，并由学生自己抽签决定具体的考试实验．小王，小张，小厉都参加了本次考试．

    ①小厉参加实验D考试的概率是　 　；

    ②用列表或画树状图的方法求小王、小张抽到同一个实验的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校研究学生的课余爱好情况，采取抽样调查的方法，从阅读、运动、娱乐、上网等四个方面调查了若干名学生的兴趣爱好，并将调查结果绘制成下面两幅不完整的统计图，请你根据图中提供的信息解答下列问题：

    （1）在这次调查中，一共调查了　 　名学生；

    （2）补全条形统计图；

    （3）若该校共有1500名学生，估计爱好运动的学生有　 　人；

    （4）在全校同学中随机选取一名学生参加演讲比赛，用频率估计概率，则选出的恰好是爱好阅读的学生的概率是　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，AB是⊙O的直径，OD⊥弦BC于点F，且交⊙O于点E，若∠AEC=∠ODB．

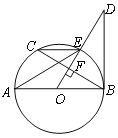
    （1）判断直线BD和⊙O的位置关系，并给出证明；

    （2）当AB=10，BC=8时，求BD的长．

    查看答案和解析>>

    同步练习册答案