
����Ŀ����ƽ��ֱ������ϵxOy�У�������y��mx2��2mx+m+4��y�ύ�ڵ�A��0��3������x�ύ�ڵ�B��C����B�ڵ�C��ࣩ��
��1����������ߵı���ʽ����B��C�����ꣻ
��2�������ߵĶԳ�����x�ύ�ڵ�D����ֱ��y��kx+b������D�͵�E����1����2������ֱ��DE�ı���ʽ��
��3���ڣ�2���������£���֪��P��t��0��������P����ֱ��x���ֱ�߽��������ڵ�M����ֱ��DE�ڵ�N������M�͵�N��������һ������x���·���ֱ��д��t��ȡֵ��Χ��
���𰸡���1��![]() ��B(-1,0)��C(3,0)����2��y=x-1����3��
��B(-1,0)��C(3,0)����2��y=x-1����3��![]() ��
��![]() ��
��
��������
���⣨1����������![]() ��y�ύ�ڵ�A��0,3������A������������ʽ�ɵó�m��ֵ������������ߵĽ���ʽ��Ȼ����������
��y�ύ�ڵ�A��0,3������A������������ʽ�ɵó�m��ֵ������������ߵĽ���ʽ��Ȼ����������![]() �ύ�ڵ�B��C���㣬�������B��C��������ꣻ��2��
�ύ�ڵ�B��C���㣬�������B��C��������ꣻ��2��
��2����![]() �����D�����꣬��D��E�ĵ����ֱ��
�����D�����꣬��D��E�ĵ����ֱ��![]() �Ľ���ʽ���������ֱ��DE�ı���ʽ��
�Ľ���ʽ���������ֱ��DE�ı���ʽ��
��3������ͼ��ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
����������⣺��1����������![]() ��y�ύ�ڵ�A��0,3����
��y�ύ�ڵ�A��0,3����
��m+4=3��
��m=-1��
�������ߵı���ʽΪ![]() ��
��
��������![]() ��
��![]() �ύ�ڵ�B��C��
�ύ�ڵ�B��C��
����y=0����![]() ��
��
���![]() ��
��![]() ��
��
������B�ڵ�C��࣬
����B������Ϊ![]() ����C������Ϊ
����C������Ϊ![]() ��
��
��2����![]() ��
��
�������ߵĶԳ���Ϊֱ��![]() ��
��
�������ߵĶԳ�����![]() �ύ�ڵ�D��
�ύ�ڵ�D��
����D������Ϊ(1,0)��
��ֱ��![]() ������D(1,0)�͵�E(-1,-2)��
������D(1,0)�͵�E(-1,-2)��
��![]()
���![]()
��ֱ��DE�ı���ʽΪy=x-1��
��3��![]() ��
��![]()


 �����ҵ��ٿ���������������ϵ�д�
�����ҵ��ٿ���������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����У�Ļ��������У����꼶һ����1��������2��Ů�����������������2��������2��Ů��������ֽ���
��1���ӻ�������������ֽ���7��ѧ����ѡȡ1���μӰ佱��ᣬ��պ��������ĸ��ʣ�
��2���ֱ�ӻ�������������ֽ���ѧ���и�ѡȡ1���μӰ佱��ᣬ���б�����״ͼ��պ���һ����һŮ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2015��2��27�գ�������ȫ����ĸ��쵼С���ʮ�λ����ϣ�����ͨ���ˡ��й�����ĸ����巽���������Ƹĸ�����ĸУ����ȳ�Ϊ�ĸ�����㣮���������棬��Ϊ�������ˮƽ�����������й��������������Ѿ������12����ͷ���г������Ѿ�����������Ĺ�ע��ͼ9��ijһ���ֹ�����ڶ��ֱ������ӵĻ���ͳ��ͼ��

(1)����ͼ������������_____֧�г���Ӳ�����
(2)��ȫͼһ�е�����ͳ��ͼ��
(3)���������������ʤһ����3�֣�ƽһ����1�֣���һ����0�֣����÷������Ϊ�ھ��������ڶ��ֱ��������λ��ǰ4���ķֱ���A��49�֣�B��49�֣�C��48�֣�D��45�֣������һ�ֵı����У����Ƿֱ�͵�4���Ժ����ӽ��б�������֪���Ѿ�������һ�������У�A�ӺͶ��ִ�ƽ�������б�������״ͼ�ķ���������C�Ӷ�ùھ��ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����10������Rt��ABC�У���BAC=![]() ,D��BC���е㣬E��AD���е�������A��AF��BC��BE���ӳ����ڵ�F��
,D��BC���е㣬E��AD���е�������A��AF��BC��BE���ӳ����ڵ�F��

��1����֤����AEF����DEB��
��2��֤���ı���ADCF�����Σ�
��3����AC=4��AB=5��������ADCFD �������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
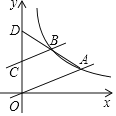
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() ��˫����
��˫����![]() ���ڵ�A������
���ڵ�A������![]() ��AO��ƽ���߽�˫�����ڵ�B������AB���ӳ���y�ύ�ڵ�
��AO��ƽ���߽�˫�����ڵ�B������AB���ӳ���y�ύ�ڵ�![]() ����k��ֵΪ______��
����k��ֵΪ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
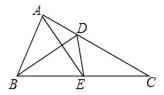
����Ŀ����ͼ������ABC�ؽ�ƽ����BD����ֱ�߷��ۣ�����Aǡ�����ڱ�BC���е�E����AE=BD����ôtan��ABD=��������
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������������y=![]() ��x��0����ͼ������OABC�ĶԽ���AC���е�M���ֱ���AB��BC���ڵ�D��E����BD=3��OA=4����k��ֵΪ_____��
��x��0����ͼ������OABC�ĶԽ���AC���е�M���ֱ���AB��BC���ڵ�D��E����BD=3��OA=4����k��ֵΪ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������
(1)��ͼ�٣�����ABC�У���A��120�㣬AB��AC��5������ABC�����Բ�뾶R��ֵΪ ��
����̽��
(2)��ͼ������O�İ뾶Ϊ13����AB��24��M��AB���е㣬P�ǡ�O��һ���㣬��PM�����ֵ��
������
(3)��ͼ����ʾ��AB��AC��BC��ij�����������滮·���У�AB��6km��AC��3km����BAC��60�㣬BC���Ե�Բ�Ľ�Ϊ60����������ί������BC·�߽�������վ��P����AB��AC·�߷ֱ����ʷ�վ��E��F��Ҳ���ǣ��ֱ���![]() ���߶�AB��AC��ѡȡ��P��E��F��������վ������Աÿ��Ҫ�������ڸ�����վ��䰴P��E��F��P��·���������䣬��ˣ�Ҫ�ڸ�����վ��֮��滮��·PE��EF��FP��Ϊ�˿�ݻ����ͽ�Լ�ɱ�Ҫʹ���߶�PE��EF��FP֮����̣�����PE��EF��FP����Сֵ(������վ�������ڵ�·֮��ľ��롢·�������Բ���)��
���߶�AB��AC��ѡȡ��P��E��F��������վ������Աÿ��Ҫ�������ڸ�����վ��䰴P��E��F��P��·���������䣬��ˣ�Ҫ�ڸ�����վ��֮��滮��·PE��EF��FP��Ϊ�˿�ݻ����ͽ�Լ�ɱ�Ҫʹ���߶�PE��EF��FP֮����̣�����PE��EF��FP����Сֵ(������վ�������ڵ�·֮��ľ��롢·�������Բ���)��



ͼ�� ͼ�� ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� �ھ���ABCD�У�AB��3��AD��4����PΪAB���ϵĶ��㣨P��A��B���غϣ�������BCP��CP���ۣ���B�Ķ�Ӧ��B1�ھ����⣬PB1��AD��E��CB1��AD�ڵ�F��
��1����ͼ1����֤����APE�ס�DFC��
��2����ͼ1�����EF��PE����BP�ij���
��3����ͼ2������BB�佻AD�ڵ�Q��EQ��QF��8��5����tan��PCB��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com