
分析 (1)将原式利用平方差公式展开,化简,最后代入求值;
(2)将原式利用平方差公式和完全平方公式展开化简,再代入求值.
解答 解:(1)原式=[3a2+(2a+1)][3a2-(2a+1)]
=(3a2)2-(2a+1)2
=9a4-(4a2+4a+1)
=9a4-4a2-4a-1,
当a=-1时,原式=9a4-4a2-4a-1
=9×(-1)4-4×(-1)2-4×(-1)+1
=9-4+4+1
=10;
(2)原式=[5a+(4b-3c)][5a-(4b-3c)]-[(a+b)2-2c(a+b)+c2]
=25a2-(4b-3c)2-(a2+2ab+b2)+2ac+2bc-c2
=25a2-16b2+24bc-9c2-a2-2ab-b2+2ac+2bc-c2
=24a2-17b2-10c2-2ab+26bc+2ac
当a=-1,b=2,c=3时,
原式=24×(-1)2-17×22-10×32-2×(-1)×2+26×2×3+2×(-1)×3
=24-68-90+4+156-6
=20.
点评 本题主要考查整式的化简求值,将原式利用公式化简是本题的关键.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:解答题
 在如图所示的方格纸中,每个小正方形的边长为1,每个小正方形的顶点都叫做格点.△ABC的顶点A、B、C都在格点上.
在如图所示的方格纸中,每个小正方形的边长为1,每个小正方形的顶点都叫做格点.△ABC的顶点A、B、C都在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-$\sqrt{5}$)2=-5 | B. | -$\sqrt{0.36}$=-0.6 | C. | $\sqrt{(-13)^{2}}$=-13 | D. | $\sqrt{36}$=±6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
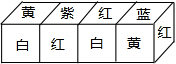 把立方体的六个面分别涂上六种不同的颜色(红、绿、蓝、黄、紫、白),现将大小相同,颜色分布完全一样的四个立方体拼成一个水平放置的长方体,如图所示,那么这个长方体中与蓝色一面相对的颜色是白色.
把立方体的六个面分别涂上六种不同的颜色(红、绿、蓝、黄、紫、白),现将大小相同,颜色分布完全一样的四个立方体拼成一个水平放置的长方体,如图所示,那么这个长方体中与蓝色一面相对的颜色是白色.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com