解:(1)如图1,过点D作DF⊥AB于F,
∵AB∥CD,∠ABC=90°,CD=4,CB=3,
∴BF=CD=4,DF=BC=3,
∵∠A=45°
∴AF=DF=3,
∴AB=AF+FB=4+3=7;
(2)设CQ=x,则PB=2x,DQ=4-x,BD=5,
当PQ⊥BD时,
易证Rt△DEQ∽Rt△DCB,
∴
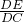
=

,即
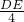
=
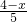
,
∴DE=

(4-x),
∴BE=5-

(4-x)=
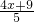
,
易证Rt△DEQ∽Rt△BEP,
∴
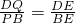
,
∴
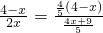
,解得
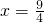
,x=4(舍去),
∴CQ=

;
(3)设CQ=x,则PB=2x,PA=7-2x,
当⊙C和⊙P外切时,如图2,PC=7-x,
在Rt△PBC中,PB
2+BC
2=PC
2,
∴4x
2+9=(7-x)
2解得:x=2,
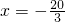
(舍去);
当⊙C和⊙P内切时,如图3,PC=7-3x,
在Rt△PBC中,PB
2+BC
2=PC
2,
∴4x
2+9=(7-3x)
2解得:
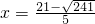
,
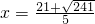
(舍去),
∴当⊙C和⊙P相切时,CQ=2或CQ=
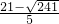
.
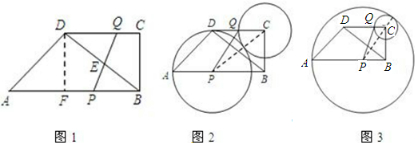
分析:(1)如图1,过点D作DF⊥AB于F,得到BF=CD=4,DF=BC=3,而∠A=45°,则AF=DF=3,即可得到AB的长;
(2)设CQ=x,则PB=2x,DQ=4-x,BD=5,当PQ⊥BD时,易证Rt△DEQ∽Rt△DCB,利用相似比可表示DE,即DE=

(4-x),则BE=5-

(4-x)=
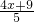
,又可证出Rt△DEQ∽Rt△BEP,利用相似比得到关于x的方程,解方程即可;
(3)设CQ=x,则PB=2x,PA=7-2x,分类讨论:当⊙C和⊙P外切时,如图2,PC=7-x,利用勾股定理得到4x
2+9=(7-x)
2;当⊙C和⊙P内切时,如图3,PC=7-3x,利用勾股定理得到4x
2+9=(7-3x)
2.然后分别解方程得到满足条件的x的值即可.
点评:本题考查了两圆相切的性质:相切两圆的圆心距等于两圆的半径之和.也考查了三角形相似的判定与性质、一元二次方程的解法以及分类讨论思想的运用.

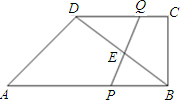 在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=4,CB=3,∠A=45°,P、Q分别是边AB、CD上的动点,(点P不与点A、B重合),且有BP=2CQ.
在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=4,CB=3,∠A=45°,P、Q分别是边AB、CD上的动点,(点P不与点A、B重合),且有BP=2CQ.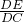 =
= ,即
,即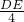 =
=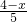 ,
, (4-x),
(4-x), (4-x)=
(4-x)=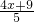 ,
,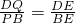 ,
,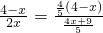 ,解得
,解得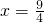 ,x=4(舍去),
,x=4(舍去), ;
;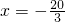 (舍去);
(舍去);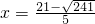 ,
,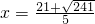 (舍去),
(舍去),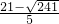 .
.
 (4-x),则BE=5-
(4-x),则BE=5- (4-x)=
(4-x)=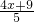 ,又可证出Rt△DEQ∽Rt△BEP,利用相似比得到关于x的方程,解方程即可;
,又可证出Rt△DEQ∽Rt△BEP,利用相似比得到关于x的方程,解方程即可;

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案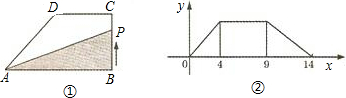
 如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为
如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为