
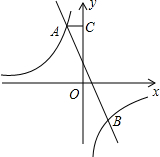
 如图,已知双曲线y=$\frac{k}{x}$和直线y=mx+n交于点A和B,B点的坐标是(2,-3),AC垂直y轴于点C,AC=$\frac{3}{2}$;
如图,已知双曲线y=$\frac{k}{x}$和直线y=mx+n交于点A和B,B点的坐标是(2,-3),AC垂直y轴于点C,AC=$\frac{3}{2}$;分析 (1)根据B在双曲线y=$\frac{k}{x}$上,B点的坐标是(2,-3),求出k值,根据AC垂直y轴于点C,AC=$\frac{3}{2}$,确定点A的横坐标,求出纵坐标,用待定系数法求出一次函数解析式;
(2)求出直线AB与x轴的交点,根据面积公式求出△AOB的面积.
解答 解:(1)∵B在双曲线y=$\frac{k}{x}$上,B点的坐标是(2,-3),
∴k=-6,∴双曲线的解析式为:y=-$\frac{6}{x}$.
∵AC垂直y轴于点C,AC=$\frac{3}{2}$,
∴点C的横坐标为-$\frac{3}{2}$,
则纵坐标为4,
设直线AB的解析式为y=kx+b,
$\left\{\begin{array}{l}{2k+b=-3}\\{-\frac{3}{2}k+b=4}\end{array}\right.$
解得$\left\{\begin{array}{l}{k=-2}\\{b=1}\end{array}\right.$
∴直线AB的解析式为y=-2x+1;
(2)直线y=-2x+1与x轴的交点坐标为($\frac{1}{2}$,0),
△AOB的面积=$\frac{1}{2}$×$\frac{1}{2}$×4+$\frac{1}{2}$×$\frac{1}{2}$×3=$\frac{7}{4}$.
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式以及观察函数图象的能力.


科目:初中数学 来源: 题型:解答题
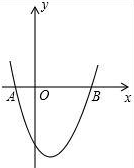 如图,抛物线y=x2-x-2交x轴于A(-1,0),B两点,交y轴于C(0,-2),过A,C画直线.点M在抛物线上,以M为圆心的圆与直线AC相切,切点为H,若⊙M的半径为$\frac{4\sqrt{5}}{5}$,求点M的坐标.
如图,抛物线y=x2-x-2交x轴于A(-1,0),B两点,交y轴于C(0,-2),过A,C画直线.点M在抛物线上,以M为圆心的圆与直线AC相切,切点为H,若⊙M的半径为$\frac{4\sqrt{5}}{5}$,求点M的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
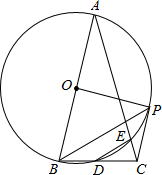 如图,在△ABC中,AB=AC,∠A=30°,以AB为直径的⊙O交BC于点D,交AC于点E,过点B作∠DBP=30°,交⊙O于点P,连接DE、CP、OP.
如图,在△ABC中,AB=AC,∠A=30°,以AB为直径的⊙O交BC于点D,交AC于点E,过点B作∠DBP=30°,交⊙O于点P,连接DE、CP、OP.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
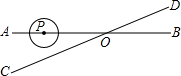 如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在射线OA上,且与点O的距离为6cm,如果⊙P以1cm/s的速度沿由A向B的方向移动,那么⊙P与直线CD相切时运动时间为( )
如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在射线OA上,且与点O的距离为6cm,如果⊙P以1cm/s的速度沿由A向B的方向移动,那么⊙P与直线CD相切时运动时间为( )| A. | 4秒 | B. | 8秒 | C. | 4秒或6秒 | D. | 4秒或8秒 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
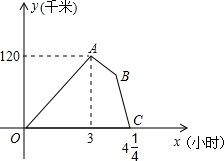 某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示.
某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.41×106 | B. | 24.1×104 | C. | 2.41×104 | D. | 2.41×105 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com