
分析 解分式方程的步骤为:①去分母;②求出整式方程的解;③检验;④得出结论.
解答 解:(1)去分母,得
(x-5)(x-1)-(x+1)(x-3)=0,
即-4x+8=0,
解得x=2,
经检验:x=2是原方程的解,
∴原方程的解为x=2;
(2)原方程可化为$\frac{5x-4}{x-2}$+1=$\frac{4x+10}{3(x-2)}$
去分母,得
15x-12+3x-6=4x+10,
解得x=2,
经检验:x=2是原方程的增根,
∴原方程无解;
(3)原方程可化为5+$\frac{96}{(x+4)(x-4)}$=$\frac{2x-1}{x+4}$+$\frac{3x-1}{x-4}$
去分母,得
5(x+4)(x-4)+96=(2x-1)(x-4)+(3x-1)(x+4),
解得x=8,
经检验:x=8是原方程的解,
∴原方程的解为x=8.
点评 本题主要考查了解分式方程,解题时注意:解分式方程时,去分母后所得整式方程的解有可能使原方程中的分母为0,所以应检验.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
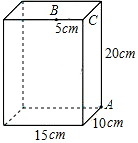 一个长方体盒子的长、宽、高分别为15cm,10cm,20cm,点B离点C的距离是5cm,一只蚂蚁想从盒底的点A沿盒的表面爬到点B,蚂蚁爬行的最短路程是( )
一个长方体盒子的长、宽、高分别为15cm,10cm,20cm,点B离点C的距离是5cm,一只蚂蚁想从盒底的点A沿盒的表面爬到点B,蚂蚁爬行的最短路程是( )| A. | 10$\sqrt{5}$cm | B. | 25cm | C. | 5$\sqrt{29}$cm | D. | 5$\sqrt{37}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
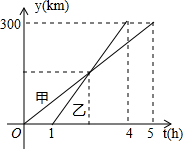 如图,甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A成的距离y(千米)与甲车行驶的时间t(时)之间的关系如图所示,观察图象回答下列问题:
如图,甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A成的距离y(千米)与甲车行驶的时间t(时)之间的关系如图所示,观察图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “该运动员两次的射击成绩都是9环”属于随机事件 | |
| B. | “该运动员一次的射击成绩为10环,一次的射击成绩为0环”属于不可能事件 | |
| C. | “该运动员两次的射击成绩的总成绩为21环”属于必然事件 | |
| D. | 该运动员一次的射击成绩大于6环的可能性比大于8环的可能性小 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 带正号的数是正数,带负号的数是负数 | |
| B. | 若|a|=a,则a一定是非负数 | |
| C. | 一个数的相反数,不是正数,就是负数 | |
| D. | 零除以任何数都等于零 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com