练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．甲、乙两人在400m环形跑道上练习跑步，甲的速度是5m/s，乙的速度是7m/s．两人站在同一起点，同时同向出发，那么当乙第一次恰好追上甲时，甲跑了1000m．

    分析 设乙第一次追上甲时用了xs，根据速度差×时间=二者距离即可得出关于x的一元一次方程，解之即可得出x的值，将其代入5x中即可得出结论．

    解答 解：设乙第一次追上甲时用了xs，
    根据题意得：（7-5）x=400，
    解得：x=200，
    ∴5x=1000．
    故答案为：1000．

    点评 本题考查了一元一次方程的应用，根据速度差×时间=二者距离列出关于x的一元一次方程是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

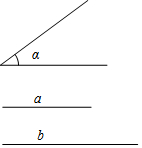    6．按要求作图（不必写作图过程，但需保留作图痕迹）．
    （1）用量角器作一个∠AOB，使得∠AOB=2∠α；
    （2）已知线段a，b，用直角和圆规作线段MN，使MN=2a-b．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．-3的相反数是3，|-3|的相反数是-3，（-1）2005=-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．（1）计算：（$\frac{1}{3}$xy）2•（-12x2y2）÷（-$\frac{4}{3}$x3y）
    （2）计算：（π-2005）0×2÷$\frac{1}{2}$+（-$\frac{1}{3}$）-2÷2-3-|8$\frac{2}{3}$-80$\frac{2}{3}$|

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．先化简，再求值
    （1）（-x2+5+4x）+（5x-4+2x2），其中x=2；
    （2）$\frac{1}{2}$a2b-5ac-（3a2c-a2b）+（3ac-4a2c），其中a=-1，b=2，c=-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．已知，正六边形ABCDEF在直角坐标系的位置如图所示，A（-1，0），点B在原点，把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转，每次翻转60°经过5次翻转之后，点B的坐标是（$\frac{11}{2}$，$\frac{\sqrt{3}}{2}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．在△ABC中，∠A=30°，∠B=45°，CD⊥AB，垂足为D，CD=6，求AB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．下列计算结果正确的是（　　）
    A．1+（-24$\frac{6}{7}$）÷（-6）=-3$\frac{1}{7}$B．-3.5÷$\frac{7}{8}$×（-$\frac{3}{4}$）-2=-5
    C．（-$\frac{3}{5}$）÷（-$\frac{9}{16}$）×16=$\frac{1}{3}$D．3-（-6）÷（-4）÷1$\frac{1}{5}$=$\frac{7}{4}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．解分式方程：
    （1）$\frac{x-5}{x-3}$-$\frac{x+1}{x-1}$=0 
    （2）$\frac{5x-4}{x-2}$+1=$\frac{4x+10}{3x-6}$．
    （3）5+$\frac{96}{{x}^{2}-16}$=$\frac{2x-1}{4+x}$-$\frac{3x-1}{4-x}$．

    查看答案和解析>>

    同步练习册答案