
| A. | 1+(-24$\frac{6}{7}$)÷(-6)=-3$\frac{1}{7}$ | B. | -3.5÷$\frac{7}{8}$×(-$\frac{3}{4}$)-2=-5 | ||
| C. | (-$\frac{3}{5}$)÷(-$\frac{9}{16}$)×16=$\frac{1}{3}$ | D. | 3-(-6)÷(-4)÷1$\frac{1}{5}$=$\frac{7}{4}$ |
分析 原式各项计算得到结果,即可作出判断.
解答 解:A、原式=1+(-$\frac{582}{7}$)×(-$\frac{1}{6}$)=1+$\frac{582}{42}$=$\frac{90}{7}$,不符合题意;
B、原式=$\frac{7}{2}$×$\frac{8}{7}$×$\frac{3}{4}$-2=3-2=1,不符合题意;
C、原式=$\frac{3}{5}$×$\frac{16}{9}$×16=$\frac{256}{15}$,不符合题意;
D、原式=3-$\frac{3}{2}$×$\frac{5}{6}$=3-$\frac{5}{4}$=$\frac{7}{4}$,符合题意,
故选D.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
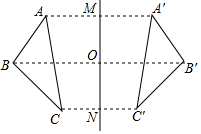 如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法不一定正确的是( )
如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法不一定正确的是( )| A. | AC=A′C′ | B. | BO=B′O | C. | AA′⊥MN | D. | AB∥B′C′ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
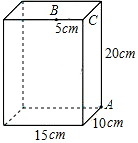 一个长方体盒子的长、宽、高分别为15cm,10cm,20cm,点B离点C的距离是5cm,一只蚂蚁想从盒底的点A沿盒的表面爬到点B,蚂蚁爬行的最短路程是( )
一个长方体盒子的长、宽、高分别为15cm,10cm,20cm,点B离点C的距离是5cm,一只蚂蚁想从盒底的点A沿盒的表面爬到点B,蚂蚁爬行的最短路程是( )| A. | 10$\sqrt{5}$cm | B. | 25cm | C. | 5$\sqrt{29}$cm | D. | 5$\sqrt{37}$cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com