
分析 设$\frac{{a}_{2}{b}^{2}}{{a}^{2}{y}^{2}+{b}^{2}{x}^{2}}$=$\frac{{b}^{2}{c}^{2}}{{b}^{2}{z}^{2}+{c}^{2}{y}^{3}}$=$\frac{{c}^{2}{d}^{2}}{{c}^{2}{w}^{2}+{d}^{2}{z}^{2}}$=$\frac{abcd}{xyzw}$=$\frac{1}{k}$,从而得$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=$\frac{{z}^{2}}{{c}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=$\frac{{w}^{2}}{{d}^{2}}$+$\frac{{z}^{2}}{{c}^{2}}$=$\frac{xyzw}{abcd}$=k,即$\frac{{x}^{2}}{{a}^{2}}$=$\frac{{z}^{2}}{{c}^{2}}$、$\frac{{y}^{2}}{{b}^{2}}$=$\frac{{w}^{2}}{{d}^{2}}$、$\frac{xyzw}{abcd}$=k,设$\frac{{x}^{2}}{{a}^{2}}$=$\frac{{z}^{2}}{{c}^{2}}$=k1、$\frac{{y}^{2}}{{b}^{2}}$=$\frac{{w}^{2}}{{d}^{2}}$=k2,从而得k=$\sqrt{{{k}_{1}}^{2}•{{k}_{2}}^{2}}$、k1+k2=k,代入即可得.
解答 解:设$\frac{{a}_{2}{b}^{2}}{{a}^{2}{y}^{2}+{b}^{2}{x}^{2}}$=$\frac{{b}^{2}{c}^{2}}{{b}^{2}{z}^{2}+{c}^{2}{y}^{3}}$=$\frac{{c}^{2}{d}^{2}}{{c}^{2}{w}^{2}+{d}^{2}{z}^{2}}$=$\frac{abcd}{xyzw}$=$\frac{1}{k}$,
则$\frac{{a}^{2}{y}^{2}+{b}^{2}{x}^{2}}{{a}^{2}{b}^{2}}$=$\frac{{b}^{2}{z}^{2}+{c}^{2}{y}^{2}}{{b}^{2}{c}^{2}}$=$\frac{{c}^{2}{w}^{2}+{d}^{2}{z}^{2}}{{c}^{2}{d}^{2}}$=$\frac{xyzw}{abcd}$=k,
整理,得:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=$\frac{{z}^{2}}{{c}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=$\frac{{w}^{2}}{{d}^{2}}$+$\frac{{z}^{2}}{{c}^{2}}$=$\frac{xyzw}{abcd}$=k,
∴$\frac{{x}^{2}}{{a}^{2}}$=$\frac{{z}^{2}}{{c}^{2}}$、$\frac{{y}^{2}}{{b}^{2}}$=$\frac{{w}^{2}}{{d}^{2}}$,$\frac{xyzw}{abcd}$=k,
设$\frac{{x}^{2}}{{a}^{2}}$=$\frac{{z}^{2}}{{c}^{2}}$=k1,$\frac{{y}^{2}}{{b}^{2}}$=$\frac{{w}^{2}}{{d}^{2}}$=k2,
由$\frac{xyzw}{abcd}$=k可得k=$\sqrt{{{k}_{1}}^{2}•{{k}_{2}}^{2}}$,
由$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=$\frac{{a}^{2}{y}^{2}+{b}^{2}{x}^{2}}{{a}^{2}{b}^{2}}$得k1+k2=k,
∴原式=2×$\frac{1}{{k}_{1}}$+2×$\frac{1}{{k}_{2}}$=$\frac{2({k}_{1}+{k}_{2})}{{k}_{1}{k}_{2}}$=2.
点评 本题主要考查分式的化简求值,熟练掌握分式的运算法则和性质是解题的关键.


科目:初中数学 来源: 题型:解答题
 +(-3xy2)=2x3-5xy2-1+x2
+(-3xy2)=2x3-5xy2-1+x2查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
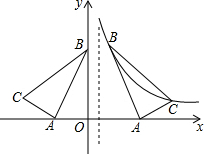 如图,在平面直角坐标系中有Rt△ABC,∠CAB=90°,A(-2,0),B(0,4),点C在第二象限且tan∠ACB=2,将Rt△ABC沿平行于y轴的某条直线翻折,得Rt△A1B1C1,若点B1,C1恰好落在反比例函数y=$\frac{k}{x}$(x>0)的图象上,则k的值等于$\frac{16}{3}$.
如图,在平面直角坐标系中有Rt△ABC,∠CAB=90°,A(-2,0),B(0,4),点C在第二象限且tan∠ACB=2,将Rt△ABC沿平行于y轴的某条直线翻折,得Rt△A1B1C1,若点B1,C1恰好落在反比例函数y=$\frac{k}{x}$(x>0)的图象上,则k的值等于$\frac{16}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1+(-24$\frac{6}{7}$)÷(-6)=-3$\frac{1}{7}$ | B. | -3.5÷$\frac{7}{8}$×(-$\frac{3}{4}$)-2=-5 | ||
| C. | (-$\frac{3}{5}$)÷(-$\frac{9}{16}$)×16=$\frac{1}{3}$ | D. | 3-(-6)÷(-4)÷1$\frac{1}{5}$=$\frac{7}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com