
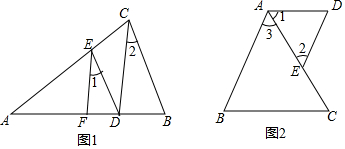
分析 (1)根据内错角相等两直线平行,可得DF∥CD,根据两直线平行,内错角相等可得∠1=∠EDC,然后求出∠EDC=∠2,再根据内错角相等,两直线平行证明即可;
(2)根据内错角相等两直线平行可得AD∥BC,根据两直线平行同旁内角互补可得∠B+∠BAD=180°,然后求出∠D+∠BAD=180°,再根据同旁内角互补两直线平行证明AB∥DE,然后根据两直线平行,内错角相等证明即可.
解答 (1)证明:∵∠AEF=∠ACD,
∴DF∥CD,
∴∠1=∠EDC,
又∵∠1=∠2,
∴∠EDC=∠2,
∴DE∥BC;
(2)证明:∵∠1=∠C,
∴AD∥BC,
∴∠B+∠BAD=180°,
∵∠B=∠D,
∴∠D+∠BAD=180°,
∴AB∥DE,
∴∠3=∠2.
点评 本题考查了平行线的判定与性质,熟记性质与平行线的判定方法并准确识图理清图中各角度之间的关系是解题的关键.


科目:初中数学 来源: 题型:解答题
 按要求作图(不必写作图过程,但需保留作图痕迹).
按要求作图(不必写作图过程,但需保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 +(-3xy2)=2x3-5xy2-1+x2
+(-3xy2)=2x3-5xy2-1+x2查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1+(-24$\frac{6}{7}$)÷(-6)=-3$\frac{1}{7}$ | B. | -3.5÷$\frac{7}{8}$×(-$\frac{3}{4}$)-2=-5 | ||
| C. | (-$\frac{3}{5}$)÷(-$\frac{9}{16}$)×16=$\frac{1}{3}$ | D. | 3-(-6)÷(-4)÷1$\frac{1}{5}$=$\frac{7}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com