
分析 先移项后配方,根据二次根式被开方数的非负性,将n的取值分两种情况进行讨论:①当n=0时,②当n≠0时,分别列式可求得三个字母的值并相加.
解答 解:|m-1|+|n+1|+$\sqrt{(m-2){n}^{2}}$+m2+p2=1+2mp,
|m-1|+|n+1|+$\sqrt{(m-2){n}^{2}}$+m2-2mp+p2=1,
|m-1|+|n+1|+$\sqrt{(m-2){n}^{2}}$+(m-p)2=1,
∵(m-2)n2≥0,
分两种情况:
①当n=0时,|m-1|+1+(m-p)2=1,
|m-1|+(m-p)2=0,
则$\left\{\begin{array}{l}{m-1=0}\\{m-p=0}\end{array}\right.$,
∴m=p=2,
∴m+n+p=1+0+1=2,
②当n≠0时,m≥2,
∴|m-1|≥1,
∵|n+1|≥0,$\sqrt{(m-2){n}^{2}}$≥0,(m-p)2≥0,
则$\left\{\begin{array}{l}{m-1=1}\\{n+1=0}\\{(m-2){n}^{2}=0}\\{m-p=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=p=2}\\{n=-1}\end{array}\right.$,
∴m+n+p=2-1+2=3;
综上所述,m+n+p的值为2或3.
点评 本题考查了配方法的应用、绝对值、平方和算术平方根的非负性,有难度,根据算术平方根的非负性分情况讨论是关键;此类题的一般思路为:把原式左边化成几个完全平方式和的形式,根据非负数和为零,各数均为零的性质求解.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:解答题
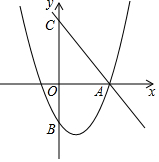 如图,直线y=-$\frac{4}{3}$x+4交x轴于点A,交y轴于点C,抛物线y=ax2-$\frac{4}{3}$x+c过点A,交y轴于点B(0,-2).
如图,直线y=-$\frac{4}{3}$x+4交x轴于点A,交y轴于点C,抛物线y=ax2-$\frac{4}{3}$x+c过点A,交y轴于点B(0,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
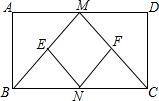 如图,在矩形ABCD中,M,N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点
如图,在矩形ABCD中,M,N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点查看答案和解析>>
科目:初中数学 来源: 题型:选择题
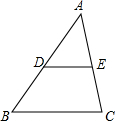 如图,已知在△ABC中,DE∥BC,BC=6,ED=2,点A到BC的距离为5,则A到DE的距离是( )
如图,已知在△ABC中,DE∥BC,BC=6,ED=2,点A到BC的距离为5,则A到DE的距离是( )| A. | $\frac{5}{6}$ | B. | $\frac{5}{3}$ | C. | $\frac{6}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
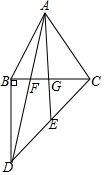 如图,在△ABC中,AB=AC,过点B作BD⊥BC,BD=BC,连接AD交BC于点F.E是CD的中点,连接AE交BC于G.
如图,在△ABC中,AB=AC,过点B作BD⊥BC,BD=BC,连接AD交BC于点F.E是CD的中点,连接AE交BC于G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
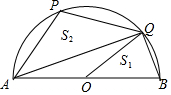 如图,在半圆O中,AB为直径,点P是圆上一点,连结AP,过O作OQ∥AP与半圆交于点Q,设△OQB的面积为S1,△APQ的面积为S2,若$\frac{{S}_{1}}{{S}_{2}}$=$\frac{5}{6}$,则tan∠PQA的值为( )
如图,在半圆O中,AB为直径,点P是圆上一点,连结AP,过O作OQ∥AP与半圆交于点Q,设△OQB的面积为S1,△APQ的面积为S2,若$\frac{{S}_{1}}{{S}_{2}}$=$\frac{5}{6}$,则tan∠PQA的值为( )| A. | $\frac{5}{6}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com