
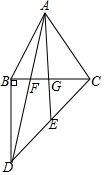
 如图,在△ABC中,AB=AC,过点B作BD⊥BC,BD=BC,连接AD交BC于点F.E是CD的中点,连接AE交BC于G.
如图,在△ABC中,AB=AC,过点B作BD⊥BC,BD=BC,连接AD交BC于点F.E是CD的中点,连接AE交BC于G.分析 (1)首先证明△ABC是等边三角形,推出∠ABC=60°,由BA=BC=BD,推出A、C、D三点在⊙B上,即可推出∠ADC=$\frac{1}{2}$∠ABC=30°.
(2)连接BE.由∠DBC=90°,DE=EC,推出BE=EC=DE,由AB=AC,推出AE垂直平分BC,推出BG=CG,设BG=CG=a,则BC=BD=2a,由BF=$\frac{1}{4}$BC,推出BF=FG,由BD∥AG,推出△BFD∽△GFA,可得$\frac{BF}{FG}$=$\frac{BD}{AG}$=1,推出BD=AG=2a,在Rt△ABG中,根据AB2=AG2+BG2,列出方程求出a即可解决问题.
解答 解:(1)如图1中,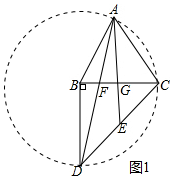
∵AB=AC,BD=BC,AB=BD,
∴AB=BC=AC,
∴△ABC是等边三角形,
∴∠ABC=60°,
∵BA=BC=BD,
∴A、C、D三点在⊙B上,
∴∠ADC=$\frac{1}{2}$∠ABC=30°.
(2)如图2中,连接BE.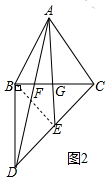
∵∠DBC=90°,DE=EC,
∴BE=EC=DE,∵AB=AC,
∴AE垂直平分BC,
∴BG=CG,设BG=CG=a,则BC=BD=2a,
∵BF=$\frac{1}{4}$BC,
∴BF=FG,
∵BD∥AG,
∴△BFD∽△GFA,
∴$\frac{BF}{FG}$=$\frac{BD}{AG}$=1,
∴BD=AG=2a,
在Rt△ABG中,∵AB2=AG2+BG2,
∴16=a2+4a2,
∴a2=$\frac{16}{5}$,
∴S四边形ABCD=$\frac{1}{2}$•BC•AG+$\frac{1}{2}$•BC•BD=$\frac{1}{2}$×2a×2a+$\frac{1}{2}$×2a×2a=4a2=$\frac{64}{5}$.
点评 本题考查等边三角形的判定和性质、相似三角形的判定和性质、勾股定理、四边形的面积、圆周角定理等知识,解题的关键是学会利用辅助圆解决角度问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 按要求作图(不必写作图过程,但需保留作图痕迹).
按要求作图(不必写作图过程,但需保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
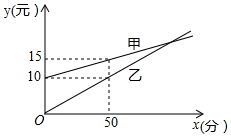 如图所示,是某电信公司甲、乙两种业务:每月通话费用y(元)与通话时间x(分)之间的函数关系.某企业的周经理想从两种业务中选择一种,如果周经理每个月的通话时间都在100分钟以上,那么选择甲种业务合算.
如图所示,是某电信公司甲、乙两种业务:每月通话费用y(元)与通话时间x(分)之间的函数关系.某企业的周经理想从两种业务中选择一种,如果周经理每个月的通话时间都在100分钟以上,那么选择甲种业务合算.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 +(-3xy2)=2x3-5xy2-1+x2
+(-3xy2)=2x3-5xy2-1+x2查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com