
分析 已知等式整理后,根据a与b为有理数求出a与b的值,即可求出a+b的值.
解答 解:已知等式整理得:5-$\sqrt{3}$a=(2b-a)+$\frac{2}{3}$$\sqrt{3}$,
可得$\left\{\begin{array}{l}{2b-a=5}\\{-a=\frac{2}{3}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{2}{3}}\\{b=\frac{13}{6}}\end{array}\right.$,
则a+b=$\frac{3}{2}$.
点评 此题考查了实数的运算,以及无理数与有理数,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:选择题
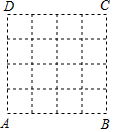 在数学活动课上,老师要求学生在4×4的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在各点上,而且三边与AB或AD都不平行,则画出的形状不同的直角三角形有( )种.
在数学活动课上,老师要求学生在4×4的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在各点上,而且三边与AB或AD都不平行,则画出的形状不同的直角三角形有( )种.| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
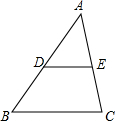 如图,已知在△ABC中,DE∥BC,BC=6,ED=2,点A到BC的距离为5,则A到DE的距离是( )
如图,已知在△ABC中,DE∥BC,BC=6,ED=2,点A到BC的距离为5,则A到DE的距离是( )| A. | $\frac{5}{6}$ | B. | $\frac{5}{3}$ | C. | $\frac{6}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
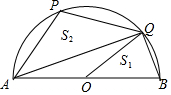 如图,在半圆O中,AB为直径,点P是圆上一点,连结AP,过O作OQ∥AP与半圆交于点Q,设△OQB的面积为S1,△APQ的面积为S2,若$\frac{{S}_{1}}{{S}_{2}}$=$\frac{5}{6}$,则tan∠PQA的值为( )
如图,在半圆O中,AB为直径,点P是圆上一点,连结AP,过O作OQ∥AP与半圆交于点Q,设△OQB的面积为S1,△APQ的面积为S2,若$\frac{{S}_{1}}{{S}_{2}}$=$\frac{5}{6}$,则tan∠PQA的值为( )| A. | $\frac{5}{6}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
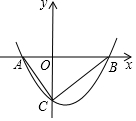 平面直角坐标系中,将抛物线y=ax2经平移后与x轴交于点A、B,与y轴交于点C,若$\frac{{{S_{△AOC}}}}{{{S_{△BOC}}}}=\frac{{\sqrt{5}-1}}{2}$,则称平移后的抛物线所在的位置为抛物线y=ax2在该平面直角坐标系中的一个“黄金位”.如图所示的抛物线为抛物线y=ax2的一个“黄金位”,且AB=2,将图中的抛物线向右平移$\frac{5+\sqrt{5}}{2}$个单位长度又可得到抛物线y=ax2的另一个“黄金位”.
平面直角坐标系中,将抛物线y=ax2经平移后与x轴交于点A、B,与y轴交于点C,若$\frac{{{S_{△AOC}}}}{{{S_{△BOC}}}}=\frac{{\sqrt{5}-1}}{2}$,则称平移后的抛物线所在的位置为抛物线y=ax2在该平面直角坐标系中的一个“黄金位”.如图所示的抛物线为抛物线y=ax2的一个“黄金位”,且AB=2,将图中的抛物线向右平移$\frac{5+\sqrt{5}}{2}$个单位长度又可得到抛物线y=ax2的另一个“黄金位”.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
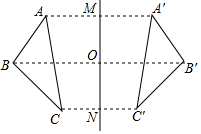 如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法不一定正确的是( )
如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法不一定正确的是( )| A. | AC=A′C′ | B. | BO=B′O | C. | AA′⊥MN | D. | AB∥B′C′ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com