
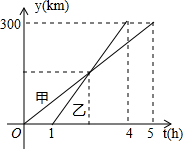
 如图,甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A成的距离y(千米)与甲车行驶的时间t(时)之间的关系如图所示,观察图象回答下列问题:
如图,甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A成的距离y(千米)与甲车行驶的时间t(时)之间的关系如图所示,观察图象回答下列问题:分析 (1)根据函数图象可以直接得到A,B两城的距离;
(2)根据函数图象中的数据可以得到若两车同时出发,乙车将比甲车早到几小时;
(3)根据函数图象中的数据可以求得乙车的速度和乙车出发几小时两车相遇;
(4)根据函数图象中的数据可以分别求得甲、乙两车对应的函数解析式,从而可以解答本题.
解答 解:(1)由图象可得,
A,B两城相距300千米,
故答案为:300;
(2)由图象可得,
若两车同时出发,乙车将比甲车早到:5-(4-1)=5-3=2(小时),
故答案为:2;
(3)由图象可得,
乙车的速度为:300÷(4-1)=100千米/时,
设乙车出发x小时时两车相遇,
$\frac{300}{5}×(x+1)=100x$,
解得,x=1.5,
故答案为:100,1.5;
(4)设甲车对应的函数解析式为y=kx,
5k=300,得k=60,
∴甲车对应的函数解析式为y=60x,
设乙车对应的函数解析式为y=ax+b,
$\left\{\begin{array}{l}{a+b=0}\\{4a+b=300}\end{array}\right.$,得$\left\{\begin{array}{l}{a=100}\\{b=-100}\end{array}\right.$,
即乙车对应的函数解析式为y=100x-100,
∴|(100x-100)-60x|=40,
解得,${x}_{1}=\frac{3}{2}$,${x}_{2}=\frac{7}{2}$,
当x=$\frac{3}{2}$时,乙出发$\frac{3}{2}-1=\frac{1}{2}$小时,
当x=$\frac{7}{2}$时,乙出发$\frac{7}{2}-1=\frac{5}{2}$小时,
即当乙车出发$\frac{1}{2}$小时或$\frac{5}{2}$小时时,甲、乙两车相距40千米.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用函数的性质数形结合的思想解答,注意第(4)问中求得是乙车出发几小时,这也是易错点,容易求出甲车出发的时间误认为是乙车出发的时间.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com