
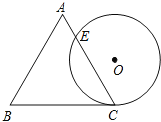
【题目】一个边长为4cm的等边三角形ABC与⊙O等高,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长为 cm.
科目:初中数学 来源: 题型:
【题目】如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.

(1)求证:△ABQ≌△CAP;
(2)如图1,当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说理由;若不变,求出它的度数.
(3)如图2,若点P、Q在分别运动到点B和点C后,继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC= 度.(直接填写度数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,垂足为E,且AB=6cm,则△DEB的周长为( )

A. 4cm B. 6cm C. 8cm D. 10cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有2个红球(记为红球1、红球2),1个白球、1个黑球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是
(2)先从中任意摸出一个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表),求两次都摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016浙江省舟山市第4题)13世纪数学家斐波那契的(计算书)中有这样一个问题:“在罗马有7位老妇人,每人赶着7头毛驴,每头驴驮着7只口袋,每只口袋里装着7个面包,每个面包附有7把餐刀,每把餐刀有7只刀鞘”,则刀鞘数为( )
A.42 B.49 C.76 D.77
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,错误的是( )
A. 一组对边平行且相等的四边形是平行四边形
B. 两条对角线互相垂直且平分的四边形是菱形
C. 四个角都相等的四边形是矩形
D. 邻边相等的菱形是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com