
马航MH370失联后,我国政府积极参与搜救.某日,我两艘专业救助船A、B同时收到有关可疑漂浮物的讯息,可疑漂浮物P在救助船A的北偏东53.50方向上,在救助船B的西北方向上,船B在船A正东方向140海里处。(参考数据:sin36.5≈0.6,cos36.5≈0.8,tan36.5≈0.75).
(1)求可疑漂浮物P到A、B两船所在直线的距离;
(2)若救助船A、救助船B分别以40海里/时,30海里/时的速度同时出发,匀速直线前往搜救,试通过计算判断哪艘船先到达P处。

(1)可疑漂浮物P到A、B两船所在直线的距离为60海里.
(2)救助船A先到达P处.

【解析】
试题分析:(1)过点P作PH⊥AB于点H,在Rt△APH中解出PH即可;
(2)在Rt△BPH中,求出BP,分别计算出两艘船需要的时间,即可作出判断.
试题解析:(1)如图,过点P作PH⊥AB于点H,则PH的长是P到A、B两船所在直线的距离.
根据题意,得∠PAH=90°-53.50°=36.5°,∠PBH=45°,AB=140海里.
设PH=x海里
在Rt△PHB中,tan45°= ,∴BH=x;
,∴BH=x;
在Rt△PHA中,tan36.5°= ,∴AH=
,∴AH= =
= x.
x.
∵AB=140,∴ x +x=140,
x +x=140,
解得x=60,即PH=60,因此可疑漂浮物P到A、B两船所在直线的距离为60海里.
在Rt△PHA中,AH= ×60=80, PA=
×60=80, PA= =100,
=100,
救助船A到达P处的时间tA=100÷40=2.5小时;
在Rt△PHB中,PB= =60
=60 ,救助船B到达P处的时间tB=60
,救助船B到达P处的时间tB=60 ÷30=2
÷30=2 小时.
小时.
∵2.5<2 ,
,
∴救助船A先到达P处.
考点:解直角三角形的应用——方向角问题.


科目:初中数学 来源:2014年初中毕业升学考试(四川成都卷)数学(解析版) 题型:解答题
如图,矩形ABCD中,AD=2AB,E是AD边上一点, (
( 为大于2的整数),连接BE,作BE的垂直平分线分别交AD、BC于点F,G,FG与BE的交点为O,连接BF和EG.
为大于2的整数),连接BE,作BE的垂直平分线分别交AD、BC于点F,G,FG与BE的交点为O,连接BF和EG.
(1)试判断四边形BFEG的形状,并说明理由;
(2)当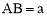 (
( 为常数),
为常数), 时,求FG的长;
时,求FG的长;
(3)记四边形BFEG的面积为 ,矩形ABCD的面积为
,矩形ABCD的面积为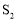 ,当
,当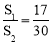 时,求
时,求 的值.(直接写出结果,不必写出解答过程)
的值.(直接写出结果,不必写出解答过程)

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川德阳卷)数学(解析版) 题型:选择题
如图,直线a∥b,∠A=38°,∠1=46°,则∠ACB的度数是( )

A.84° B.106° C.96° D.104°
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川宜宾卷)数学(解析版) 题型:选择题
下列运算的结果中,是正数的是( )
A.(﹣2014)﹣1 B.﹣(2014)﹣1
C.(﹣1)×(﹣2014) D.(﹣2014)÷2014
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川南充卷)数学(解析版) 题型:选择题
二次函数 =
= (
( ≠0)图象如图所示,下列结论:①
≠0)图象如图所示,下列结论:① >0;②
>0;② =0;③当
=0;③当 ≠1时,
≠1时, >
> ;④
;④ >0;⑤若
>0;⑤若 =
= ,且
,且 ≠
≠ ,则
,则 =2.其中正确的有( )
=2.其中正确的有( )
A.①②③ B.②④ C.②⑤ D.②③⑤

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川内江卷)数学(解析版) 题型:解答题
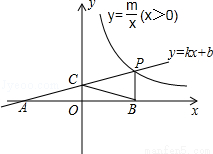
如图,一次函数y=kx+b的图象与反比例函数y= (x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(1)求一次函数、反比例函数的解析式;
(2)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,求出点D的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(吉林卷)数学(解析版) 题型:选择题
如图,△ABC中,∠C=45°,点D在AB上,点E在BC上.若AD=DB=DE,AE=1,则AC的长为( )

A. B.2 C.
B.2 C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com