
【题目】矩形ABCD中AB=5,AD=3,将矩形ABCD绕点C顺时针旋转至矩形EFCG(其中A、B、D分别与E、F、G对应).

(1)如图1,当点G落在AB边上时,求AG的长;
(2)如图2.当点G落在线段AE上时,AB与CG交于点H,求BH;
(3)如图3,记O为矩形ABCD的对角线交点,S为△OGE的面积,直接写出s的取值范围.
【答案】(1)1;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)在Rt△BCG中,利用勾股定理求出BG即可解决问题;
(2)首先证明AH=CH,设AH=CH=m,则BH=5m,在Rt△BHC中,根据CH2=BC2+BH2,构建方程求出m即可解决问题;
(3)如图,当点G在对角线AC上时,△OGE的面积最小,当点G在AC的延长线上时,△OE′G′的面积最大,分别求出面积的最小值,最大值即可解决问题.
(1)如图1中,
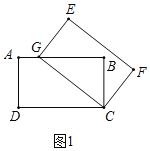
∵四边形ABCD是矩形,
∴AB=CD=CG=5,∠B=90°,
∵BC=AD=3,
∴![]() ,
,
∴AG=AB-BG=1;
(2)如图2中,

由四边形CGEF是矩形,得到∠CGE=90°,
∵点G在线段AE上,
∴∠AGC=90°,
∵CA=CA,CD=CG,
∴Rt△ACG≌Rt△ACD(HL).
∴∠ACD=∠ACG,
∵AB∥CD
∴∠ACD=∠BAC,
∴∠ACG =∠BAC,
∴AH=CH,
设AH=CH=m,
则BH=5-m,
在Rt△BHC中,∵CH2=BC2+BH2,
∴m2=32+(5-m)2,
∴![]() ,
,
∴![]() ;
;
(3)如图,

∵AB=5,AD=3,
∴AC=![]() ,
,
当点G在对角线AC上时,△OGE的面积最小,
最小值 ;
;
当点G在AC的延长线上时,△OE′G′的面积最大,
最大值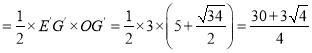
综上所述,![]() .
.


科目:初中数学 来源: 题型:
【题目】在下列网格图中,每个小正方形的边长均为1个单位.在Rt△ABC中,∠C=90°,AC=3,BC=2.
(1)试在图中画出将△ABC以B为旋转中心,沿顺时针方向旋转90°后的图形△A1BC1;
(2)若点B的坐标为(-1,-4),点C的坐标为(-3,-4),试在图中画出直角坐标系,并写出点A的坐标;
(3)根据(2)的坐标系作出与△ABC关于原点对称的图形△A2B2C2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠A=100°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC=( )
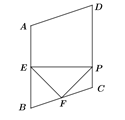
A. 55°B. 65°C. 50°D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线y=x+b与双曲线y=![]() (x<0)交于点A(﹣1,﹣5),并分别与x轴、y轴交于点C、B.
(x<0)交于点A(﹣1,﹣5),并分别与x轴、y轴交于点C、B.
(1)求出b、m的值;
(2)点D在x轴的正半轴上,若以点D、C、B组成的三角形与△OAB相似,试求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC,BC在直线MN上.
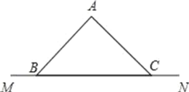
(1)根据下列要求补完整图形,
①画出△ABC关于直线MN对称的三角形A′BC;
②在线段BC上取两点D、E(![]() ,
,![]() ),使BD=CE,连接AD、AE、A′D、A′E;
),使BD=CE,连接AD、AE、A′D、A′E;
(2)求证:四边形ADA′E是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对某一个函数给出如下定义:如果存在常数![]() ,对于任意的函数值
,对于任意的函数值![]() ,都满足
,都满足![]() ≤
≤![]() ,那么称这个函数是有上界函数;在所有满足条件的
,那么称这个函数是有上界函数;在所有满足条件的![]() 中,其最小值称为这个函数的上确界.例如,函数
中,其最小值称为这个函数的上确界.例如,函数![]() ,
, ![]() ≤2,因此是有上界函数,其上确界是2.如果函数
≤2,因此是有上界函数,其上确界是2.如果函数![]() (
(![]() ≤x≤
≤x≤![]() ,
, ![]() <
<![]() )的上确界是
)的上确界是![]() ,且这个函数的最小值不超过2
,且这个函数的最小值不超过2![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() ≤
≤![]() B.
B. ![]() C.
C. ![]() ≤
≤![]() D.
D. ![]() ≤
≤![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场推销一种书包,进价为30元,在试销中发现这种书包每天的销售量P(个)与每个书包销售价x(元)满足一次函数关系式.当定价为35元时,每天销售30个;定价为40元时,每天销售20个.
(1)求P关于x的函数关系式;
(2)如果要保证商场每天销售这种书包获利200元,求书包的销售单价应定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com