
| A. | $\frac{2013}{2014}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2014}{4030}$ | D. | $\frac{2016}{4030}$ |
分析 利用平方差公式因式分解,进一步整理利用分子分母交错约分得出答案即可.
解答 解:原式=(1-$\frac{1}{2}$)(1+$\frac{1}{2}$)(1-$\frac{1}{3}$)(1+$\frac{1}{3}$)…(1-$\frac{1}{2014}$)(1+$\frac{1}{2014}$)(1-$\frac{1}{2015}$)(1+$\frac{1}{2015}$)
=$\frac{1}{2}$×$\frac{3}{2}$×$\frac{2}{3}$×$\frac{4}{3}$×…×$\frac{2013}{2014}$×$\frac{2015}{2014}$×$\frac{2016}{2015}$
=$\frac{1}{2}$×$\frac{2016}{2015}$
=$\frac{2016}{4030}$.
故选:D.
点评 此题考查因式分解的实际运用,掌握平方差公式是解决问题的关键.


科目:初中数学 来源: 题型:解答题
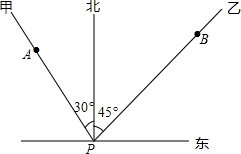 如图,点P表示某港口的位置,甲船在港口北偏西30°方向距港口50海里的A处,乙船在港口北偏东45°方向距港口60海里的B处,两船同时出发分别沿AP,BP方向匀速驶向港口P,1小时后乙船在甲船的正东方向处,已知甲船的速度是10海里/时,求乙船的速度.
如图,点P表示某港口的位置,甲船在港口北偏西30°方向距港口50海里的A处,乙船在港口北偏东45°方向距港口60海里的B处,两船同时出发分别沿AP,BP方向匀速驶向港口P,1小时后乙船在甲船的正东方向处,已知甲船的速度是10海里/时,求乙船的速度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
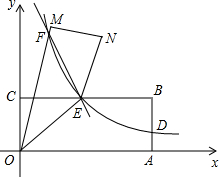 如图,矩形OABC在第一象限,OA=a,OC=b,双曲线y=$\frac{k}{x}$(x>0)始终经过BC的中点E,且与AB交于点D,连接OE.
如图,矩形OABC在第一象限,OA=a,OC=b,双曲线y=$\frac{k}{x}$(x>0)始终经过BC的中点E,且与AB交于点D,连接OE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com