
【题目】提出问题
若矩形的面积为9,则该矩形的周长有无最大值或最小值?若有,最大(小)值是多少?
分析问题
若设该矩形的长为![]() ,则矩形的宽为
,则矩形的宽为![]() ,若周长为
,若周长为![]() ,则
,则![]() 与
与![]() 的函数关系式为
的函数关系式为![]() ,问题就转化为研究该函数的最值问题.
,问题就转化为研究该函数的最值问题.
解决问题
“数学兴趣小组”对函数![]() 的最值问题进行了探究,探究过程如下:
的最值问题进行了探究,探究过程如下:
(1)填写下表,并用描点法在坐标系中画出函数![]() 的图象,
的图象,
|
| 1 | 2 | 3 | 4 | 5 |
|
|
| 20 |
| 12 |
|
|
|
其中![]() __________;
__________;
(2)观察该函数的图象,当![]() __________时,函数
__________时,函数![]() 有最__________值(填“大”或“小”),其最值是__________;
有最__________值(填“大”或“小”),其最值是__________;
(3)在求二次函数![]() 的最大(小)值时,我们可以通过配方的形式将函数表达式变为顶点式求出最值,同样函数
的最大(小)值时,我们可以通过配方的形式将函数表达式变为顶点式求出最值,同样函数![]() 也可以通过配方求最值:
也可以通过配方求最值:
![]()
![]()
![]() 当
当![]() 时,即
时,即![]() 时,
时,![]() .
.
请类比上面配方法,验证我们对该函数![]() 的最值的猜想.
的最值的猜想.
科目:初中数学 来源: 题型:
【题目】某工艺品店购进A,B两种工艺品,已知这两种工艺品的单价之和为200元,购进2个A种工艺品和3个B种工艺品需花费520元.
(1)求A,B两种工艺品的单价;
(2)该店主欲用9600元用于进货,且最多购进A种工艺品36个,B种工艺品的数量不超过A种工艺品的2倍,则共有几种进货方案?
(3)已知售出一个A种工艺品可获利10元,售出一个B种工艺品可获利18元,该店主决定每售出一个B种工艺品,为希望工程捐款m元,在(2)的条件下,若A,B两种工艺品全部售出后所有方案获利均相同,则m的值是多少?此时店主可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
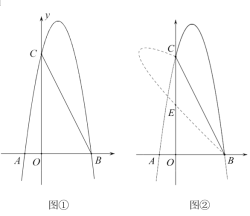
【题目】如图①,抛物线![]() 过
过![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.
(1)求该抛物线的表达式和对称轴;
(2)点![]() 是抛物线对称轴上一动点,当
是抛物线对称轴上一动点,当![]() 是以
是以![]() 为直角边的直角三角形时,求所有符合条件的点
为直角边的直角三角形时,求所有符合条件的点![]() 的坐标;
的坐标;
(3)如图②,将抛物线在![]() 上方的图象沿
上方的图象沿![]() 折叠后与
折叠后与![]() 轴交与点
轴交与点![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了开展“阳光体育运动”,计划购买篮球和足球.已知购买20个篮球和40个足球的总金额为4600元;购买30个篮球和50个足球的总金额为6100元.
(1)每个篮球、每个足球的价格分别为多少元?
(2)若该校购买篮球和足球共60个,且购买篮球的总金额不超过购买足球的总金额,则该校最多可购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
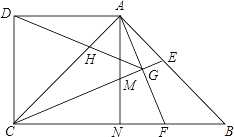
【题目】如图,在四边形 ABCD 中,AD ∥ BC ,∠BCD=90° ,∠ABC=45° ,AD=CD ,CE 平分 ∠ ACB 交 AB 于点 E ,在 BC 上截取 BF=AE ,连接 AF 交 CE 于点 G ,连接 DG 交 AC 于点 H ,过点 A 作 AN ⊥ BC ,垂足为 N , AN 交 CE 于点 M .则下列结论:① CM=AF ; ② CE ⊥ AF ; ③△ ABF ∽△ DAH ;④ GD 平分 ∠ AGC ,其中正确的序号是 ________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列问题:
(1)阅读理解:
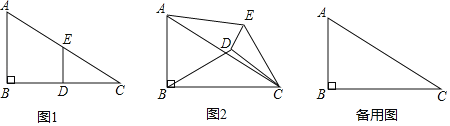
如图1,在![]() 中,若
中,若![]() ,
,![]() ,求
,求![]() 边上的中线
边上的中线![]() 的取值范围.
的取值范围.
解决此问题可以用如下方法:延长![]() 到点
到点![]() 使
使![]() ,再连接
,再连接![]() (或将
(或将![]() 绕着
绕着![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,把
,把![]() 、
、![]() ,
,![]() 集中在
集中在![]() 中,利用三角形三边的关系即可判断.中线
中,利用三角形三边的关系即可判断.中线![]() 的取值范围是______.
的取值范围是______.
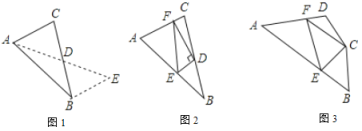
(2)问题解决:
如图2,在![]() 中,
中,![]() 是
是![]() 边上的中点,
边上的中点,![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]() .
.
(3)问题拓展:
如图3,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,以
,以![]() 为顶点作一个
为顶点作一个![]() 角,角的两边分别交
角,角的两边分别交![]() ,
,![]() 于
于![]() 、
、![]() 两点,连接
两点,连接![]() ,探索线段
,探索线段![]() ,
,![]() ,
,![]() 之间的数量关系,并加以证明.
之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
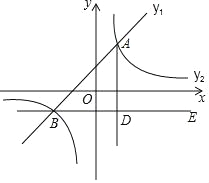
【题目】如图,在平面直角坐标系中,一次函数y1=ax+b的图象与反比例函数y2=![]() 的图象交于点A(1,2)和B(﹣2,m).
的图象交于点A(1,2)和B(﹣2,m).
(1)求一次函数和反比例函数的表达式;
(2)请直接写出y1≥y2时x的取值范围;
(3)过点B作BE∥x轴,AD⊥BE于点D,点C是直线BE上一点,若∠DAC=30°,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
背景阅读:旋转就是将图形上的每一点在平面内绕着旋转中心旋转固定角度的位置移动,其中“旋”是过程,“转”是结果.旋转作为图形变换的一种,具备图形旋转前后对应点到旋转中心的距离相等:对应点与旋转中心所连线段的夹角等于旋转角:旋转前、后的图形是全等图形等性质.所以充分运用这些性质是在解决有关旋转问题的关健.
实践操作:如图1,在Rt△ABC中,∠B=90°,BC=2AB=12,点D,E分别是边BC,AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.
问题解决:(1)①当α=0°时,![]() = ;②当α=180°时,
= ;②当α=180°时,![]() = .
= .
(2)试判断:当0°≤a<360°时,![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
问题再探:(3)当△EDC旋转至A,D,E三点共线时,求得线段BD的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com