
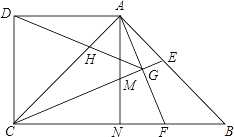
【题目】如图,在四边形 ABCD 中,AD ∥ BC ,∠BCD=90° ,∠ABC=45° ,AD=CD ,CE 平分 ∠ ACB 交 AB 于点 E ,在 BC 上截取 BF=AE ,连接 AF 交 CE 于点 G ,连接 DG 交 AC 于点 H ,过点 A 作 AN ⊥ BC ,垂足为 N , AN 交 CE 于点 M .则下列结论:① CM=AF ; ② CE ⊥ AF ; ③△ ABF ∽△ DAH ;④ GD 平分 ∠ AGC ,其中正确的序号是 ________ .
【答案】①②③④
【解析】
结论 ① 正确,证明 △ ACM ≌△ ABF 即可;结论 ② 正确,由 △ ACM ≌△ ABF 得出 ∠ 2= ∠ 4 ,进而得 ∠ 4+∠ 6=90° ,即 CE ⊥ AF ,结论 ③ 正确,证法一:利用四点共圆;证法二:利用三角形全等;结论 ④ 正确,证法一:利用四点共圆,证法二:利用三角形全等.
解:
![]()
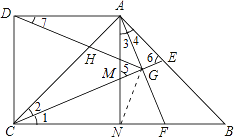
⑴ 结论 ① 正确.理由如下:
∵∠1=∠2 , ∠1+∠CMN=90° ,∠2+∠6=90° ,
∴∠6=∠CMN ,![]()
又 ∵∠5=∠CMN ,
∴∠5= ∠6 ,
∴ AM=AE=BF .
∵∠BCD=90° ,AN⊥BC,垂足为 N,
∴AN∥CD,
∵AD∥BC∴四边形ADCN是平行四边形,
∵∠BCD=90°,AD=CD
∴ ADCN 为正方形,△ ABC为等腰直角三角形,
∴ AB=AC .
在△ ACM与△ ABF 中,
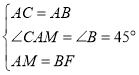 ,
,
∴△ACM ≌△ABF(SAS),
∴ CM=AF ;
⑵ 结论②正确.理由如下:
∵△ACM ≌△ABF ,
∴∠2=∠4 ,
∵∠2+∠6=90° ,
∴∠4+∠6=90° ,
∴ CE⊥AF ;
⑶ 结论③正确.理由如下:
证法一: ∵CE⊥AF ,
∴∠ADC+∠AGC=180° ,
∴ A 、D 、C 、G 四点共圆,
∴∠7=∠2 ,
∵∠2=∠4 ,
∴∠7=∠4 ,
又 ∵∠DAH=∠B=45° ,
∴△ABF∽△DAH ;
证法二: ∵ CE⊥AF, ∠1=∠2 ,
∴△ACF为等腰三角形,AC=CF,点G为AF中点.
在 Rt△ANF中,点G为斜边AF中点,
∴ NG=AG ,
∴∠MNG=∠3 ,
∴∠DAG=∠CNG .
在△ADG与△NCG 中,
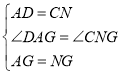 ,
,
∴△ADG≌△NCG ( SAS),
∴∠7=∠1 ,
又 ∵∠1=∠2=∠4 ,
∴∠7=∠4 ,
又 ∵∠DAH=∠B=45° ,
∴△ABF∽△DAH ;
⑷ 结论④正确.理由如下:
证法一: ∵ A、D、C、G 四点共圆,
∴∠DGC=∠DAC=45° , ∠DGA=∠DCA=45° ,
∴∠DGC=∠DGA ,即GD平分∠AGC .
证法二: ∵ AM=AE ,CE⊥AF ,
∴∠3=∠4 ,又 ∠2=∠4 , ∴∠3=∠2
则 ∠CGN=180°-∠ 1- 90°-∠MNG=180°﹣∠1﹣90°﹣∠3=90°-∠1-∠2=45° .
∵△ADG ≌△NCG ,
∴∠DGA=∠CGN=45°=![]() ∠AGC ,
∠AGC ,
∴ GD平分∠AGC .
综上所述,正确的结论是:①②③④,共 4 个.
故答案为: ①②③④


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点O与平面直角坐标系的原点重合,点A,C分别在x轴,y轴上,点B的坐标为(-5,4),点D为边BC上一点,连接OD,若线段OD绕点D顺时针旋转90°后,点O恰好落在AB边上的点E处,则点E的坐标为( )

A. (-5,3) B. (-5,4) C. (-5,![]() ) D. (-5,2)
) D. (-5,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文化是一个国家、一个民族的灵魂,近年来,央视推出《中国诗词大会》、《中国成语大会》、《朗读者》、《经曲咏流传》等一系列文化栏目.为了解学生对这些栏目的喜爱情况,某学校组织学生会成员随机抽取了部分学生进行调查,被调查的学生必须从《经曲咏流传》(记为A)、《中国诗词大会》(记为B)、《中国成语大会》(记为C)、《朗读者》(记为D)中选择自己最喜爱的一个栏目,也可以不选以上四类而写出一个自己最喜爱的其他文化栏目(这时记为E).根据调查结果绘制成如图所示的两幅不完整的统计图.
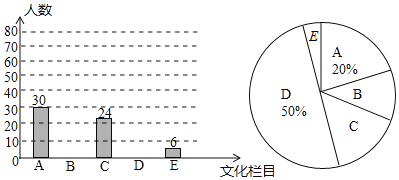
请根据图中信息解答下列问题:
(1)在这项调查中,共调查了 名学生;
(2)最喜爱《朗读者》的学生有 名;
(3)扇形统计图中“B”所在扇形圆心角的度数为 ;
(4)选择“E”的学生中有2名女生,其余为男生,现从选择“E”的学生中随机选出两名学生参加座谈,请直接写出:刚好选到一名男生和一名女生的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
材料一:对实数a、b,定义![]() 的含义为:当
的含义为:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .例如:
.例如:![]() ;
;![]() .
.
材料二:关于数学家高斯的故事,200多年前,高斯的算术老师提出了下面的问:![]() 据说,当其他同学忙于把100个数逐项相加时,十岁的高斯却用下面的方法迅速算出了正确答案:
据说,当其他同学忙于把100个数逐项相加时,十岁的高斯却用下面的方法迅速算出了正确答案:![]() .也可以这样理解:令
.也可以这样理解:令![]() ①,则
①,则![]() ②,①+②:
②,①+②:![]() ,即
,即![]() .
.
根据以上材料,回答下列问题:
(1)已知![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(2)已知![]() ,且
,且![]() ,化简:
,化简:![]() ;
;
(3)对于正数m,有![]() ,求
,求![]() …+
…+![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】提出问题
若矩形的面积为9,则该矩形的周长有无最大值或最小值?若有,最大(小)值是多少?
分析问题
若设该矩形的长为![]() ,则矩形的宽为
,则矩形的宽为![]() ,若周长为
,若周长为![]() ,则
,则![]() 与
与![]() 的函数关系式为
的函数关系式为![]() ,问题就转化为研究该函数的最值问题.
,问题就转化为研究该函数的最值问题.
解决问题
“数学兴趣小组”对函数![]() 的最值问题进行了探究,探究过程如下:
的最值问题进行了探究,探究过程如下:
(1)填写下表,并用描点法在坐标系中画出函数![]() 的图象,
的图象,
|
| 1 | 2 | 3 | 4 | 5 |
|
|
| 20 |
| 12 |
|
|
|
其中![]() __________;
__________;
(2)观察该函数的图象,当![]() __________时,函数
__________时,函数![]() 有最__________值(填“大”或“小”),其最值是__________;
有最__________值(填“大”或“小”),其最值是__________;
(3)在求二次函数![]() 的最大(小)值时,我们可以通过配方的形式将函数表达式变为顶点式求出最值,同样函数
的最大(小)值时,我们可以通过配方的形式将函数表达式变为顶点式求出最值,同样函数![]() 也可以通过配方求最值:
也可以通过配方求最值:
![]()
![]()
![]() 当
当![]() 时,即
时,即![]() 时,
时,![]() .
.
请类比上面配方法,验证我们对该函数![]() 的最值的猜想.
的最值的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, AB 是 ⊙ O 的直径, C 是![]() 的中点, CE ⊥ AB 于 E , BD 交 CE 于 F .
的中点, CE ⊥ AB 于 E , BD 交 CE 于 F .
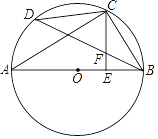
(1)求证: CF=BF ;
(2)若 CD=6 ,AC=8 ,求 BE 、 CF 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
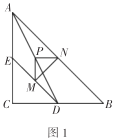
问题情境:在综合与实践课上,老师让同学们以“两个大小不等的等腰直角三角板的直角顶点重合,并让一个三角板固定,另一个绕直角顶点旋转”为主题开展数学活动,如图1,三角板![]() 和三角板
和三角板![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,连接
上,连接![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点.试判断线段
的中点.试判断线段![]() 与
与![]() 的数量关系和位置关系.
的数量关系和位置关系.
探究展示:勤奋小组发现,![]() ,
,![]() .并展示了如下的证明方法:
.并展示了如下的证明方法:
∵点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,∴
的中点,∴![]() ,
,![]() .
.
∵点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,∴
的中点,∴![]() ,
,![]() .(依据1)
.(依据1)
∵![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .(依据2)
.(依据2)
∴![]() .∴
.∴![]() .
.
反思交流:
(1)①上述证明过程中的“依据1”,“依据2”分别是指什么?
②试判断图1中,![]() 与
与![]() 的位置关系,请直接回答,不必证明;
的位置关系,请直接回答,不必证明;
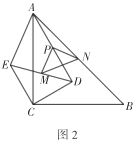
(2)创新小组受到勤奋小组的启发,继续进行探究,把![]() 绕点
绕点![]() 逆时针方向旋转到如图2的位置,发现
逆时针方向旋转到如图2的位置,发现![]() 是等腰直角三角形,请你给出证明;
是等腰直角三角形,请你给出证明;
(3)缜密小组的同学继续探究,把![]() 绕点
绕点![]() 在平面内自由旋转,当
在平面内自由旋转,当![]() ,
,![]() 时,求
时,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全球已经进入大数据时代,大数据(bigdata),是指数据规模巨大,类型多样且信息传播速度快的数据库体系.大数据在推动经济发展,改善公共服务等方面日益显示出巨大的价值.为创建大数据应用示范城市,我市某机构针对市民最关心的四类生活信息进行了民意调查(被调查者每人限选一项),下面是部分四类生活信息关注度统计图表,请根据图中提供的信息解答下列问题:
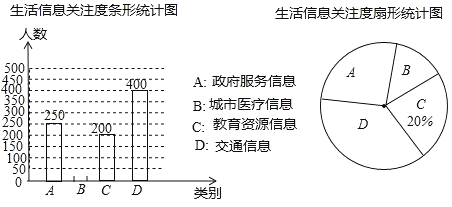
(1)本次参与调查的人数是 ,扇形统计图中D部分的圆心角的度数是 ;
(2)关注城市医疗信息的有多少人?并补全条形统计图;
(3)写出两条你从统计图中获取的信息.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B的对应点E落在坐标平面内,当△ADE是等腰直角三角形时,点E的坐标为______.
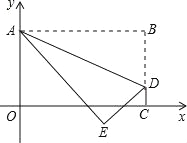
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com