
【题目】如图, AB 是 ⊙ O 的直径, C 是![]() 的中点, CE ⊥ AB 于 E , BD 交 CE 于 F .
的中点, CE ⊥ AB 于 E , BD 交 CE 于 F .
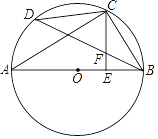
(1)求证: CF=BF ;
(2)若 CD=6 ,AC=8 ,求 BE 、 CF 的长.
【答案】(1)见解析;(2)3.6 ,![]()
【解析】
(1)延长CE交⊙O于点 P,根据垂径定理得出及圆周角定理得出 ∠BCP=∠BDC ,又由C 是![]() 的中点,得∠BDC=∠CBD ,进而得出∠CBD=∠BCP ,从而得出结论;
的中点,得∠BDC=∠CBD ,进而得出∠CBD=∠BCP ,从而得出结论;
(2)根据圆周角定理及勾股定理得出 AB 的长,再由直角三角形相似,推出对应边成比例,得出 BE 及 CE 的长,设 CF=x ,则 FE=4.8﹣x , BF=x ,根据勾股定理得出方程求解即可.
(1)证明:延长 CE 交 ⊙ O 于点 P ,
∵ CE ⊥ AB ,∴![]() ,
,
∴∠ BCP= ∠ BDC ,
∵ C 是![]() 的中点,
的中点,
∴ CD=CB ,
∴∠ BDC= ∠ CBD ,
∴∠ CBD= ∠ BCP ,
∴ CF=BF ;
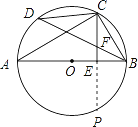
(2) ∵ CD=6 , AC=8 ,
∴ AB=10 ,
∵CF⊥AB,AC⊥BC, ∠CBA=∠EBC
∴△CBA∽△EBC
∴![]()
∴ BE= ![]() =3.6 ,
=3.6 ,
同理![]()
∴![]()
∴![]()
设 CF=x ,则 FE=4.8- x , BF=x ,
∵EF2+BE2=BF2
∴ (4.8﹣x)2 +3.62 =x2 ,
∴ x= ![]()
∴ CF=![]() .
.


科目:初中数学 来源: 题型:
【题目】每年5月的第二个星期日即为母亲节,“父母恩深重,恩怜无歇时”,许多市民喜欢在母亲节为母亲送花,感恩母亲,祝福母亲.今年节日前夕,某花店采购了一批鲜花礼盒,经分析上一年的销售情况,发现该鲜花礼盒的该周销售量y(盒)是销售单价x(元)的一次函数,已知销售单价为70元/盒时,销售量为160盒;销售单价为80元/盒时,销售量为140盒.
(1)求该周销售量y(盒)关于销售单价x(元)的一次函数解析式;
(2)若按去年方式销售,已知今年该鲜花礼盒的进价是每盒50元,商家要求该周至少要卖110盒,请你帮店长算一算,要完成商家的销售任务,销售单价不能超过多少元?
(3)在(2)的条件下,试确定销售单价x为何值时,花店该周销售鲜花礼盒获得的利润最大?并求出获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
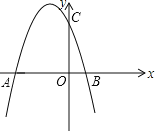
【题目】如图,抛物线y=ax2+bx+3与x轴交于A(﹣3,0),B(l,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)点P是抛物线上的动点,且满足S△PAO=2S△PCO,求出P点的坐标;
(3)连接BC,点E是x轴一动点,点F是抛物线上一动点,若以B、C、E、F为顶点的四边形是平行四边形时,请直接写出点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
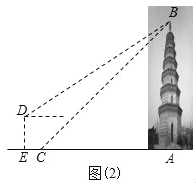
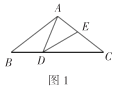
【题目】如图(1),在豫西南邓州市大十字街西南方,耸立着一座古老建筑-福胜寺梵塔,建于北宋天圣十年(公元1032年),学完了三角函数知识后,某校“数学社团”的刘明和王华决定用自己学到的知识测量“福胜寺梵塔”的高度.如图(2),刘明在点C处测得塔顶B的仰角为45°,王华在高台上的点D处测得塔顶B的仰角为40°,若高台DE高为5米,点D到点C的水平距离EC为1.3米,且A、C、E三点共线,求该塔AB的高度.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
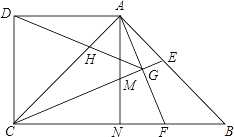
【题目】如图,在四边形 ABCD 中,AD ∥ BC ,∠BCD=90° ,∠ABC=45° ,AD=CD ,CE 平分 ∠ ACB 交 AB 于点 E ,在 BC 上截取 BF=AE ,连接 AF 交 CE 于点 G ,连接 DG 交 AC 于点 H ,过点 A 作 AN ⊥ BC ,垂足为 N , AN 交 CE 于点 M .则下列结论:① CM=AF ; ② CE ⊥ AF ; ③△ ABF ∽△ DAH ;④ GD 平分 ∠ AGC ,其中正确的序号是 ________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上的一个动点(不与
边上的一个动点(不与![]() ,
,![]() 重合),以
重合),以![]() 为边作
为边作![]() ,交
,交![]() 边于点
边于点![]() .设
.设![]() ,
,![]() .今天我们将根据学习函数的经验,研究函数值
.今天我们将根据学习函数的经验,研究函数值![]() 随自变量
随自变量![]() 的变化而变化的规律.
的变化而变化的规律.
下面是某同学做的一部分研究结果,请你一起参与解答:
(1)自变量![]() 的取值范围是 ;
的取值范围是 ;
(2)通过计算,得到![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0.5 | 1 | 1.5 | 2 | 3 | 4 | 4.5 | 5 | 5.5 |
| 3.3125 | 2.75 | 2.3125 | 2 | 2.3125 | 2.75 | 3.3125 |
请你补全表格;
(3)在如图2所示的平面直角坐标系中,画出该函数的大致图象;
(4)根据图象,请写出该函数的一条性质.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( )

A. π B. ![]() C. 3+π D. 8﹣π
C. 3+π D. 8﹣π
查看答案和解析>>
科目:初中数学 来源: 题型:
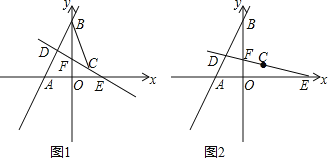
【题目】在平面直角坐标系xOy中,直线l1:y=k1x+6与x轴、y轴分别交于A、B两点,且OB=![]() OA,直线l2:y=k2x+b经过点C(
OA,直线l2:y=k2x+b经过点C(![]() ,1),与x轴、y轴、直线AB分别交于点E、F、D三点.
,1),与x轴、y轴、直线AB分别交于点E、F、D三点.
(1)求直线l1的解析式;
(2)如图1,连接CB,当CD⊥AB时,求点D的坐标和△BCD的面积;
(3)如图2,当点D在直线AB上运动时,在坐标轴上是否存在点Q,使△QCD是以CD为底边的等腰直角三角形?若存在,请直接写出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,在同一条公路上,匀速行驶,相向而行,到两车相遇时停止.甲车行驶一段时间后,因故停车0.5小时,故障解除后,继续以原速向B地行驶,两车之间的路程y(千米)与出发后所用时间x(小时)之间的函数关系如图所示.

(1)求甲、乙两车行驶的速度V甲、V乙.
(2)求m的值.
(3)若甲车没有故障停车,求可以提前多长时间两车相遇.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com