
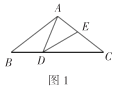
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上的一个动点(不与
边上的一个动点(不与![]() ,
,![]() 重合),以
重合),以![]() 为边作
为边作![]() ,交
,交![]() 边于点
边于点![]() .设
.设![]() ,
,![]() .今天我们将根据学习函数的经验,研究函数值
.今天我们将根据学习函数的经验,研究函数值![]() 随自变量
随自变量![]() 的变化而变化的规律.
的变化而变化的规律.
下面是某同学做的一部分研究结果,请你一起参与解答:
(1)自变量![]() 的取值范围是 ;
的取值范围是 ;
(2)通过计算,得到![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0.5 | 1 | 1.5 | 2 | 3 | 4 | 4.5 | 5 | 5.5 |
| 3.3125 | 2.75 | 2.3125 | 2 | 2.3125 | 2.75 | 3.3125 |
请你补全表格;
(3)在如图2所示的平面直角坐标系中,画出该函数的大致图象;
(4)根据图象,请写出该函数的一条性质.
【答案】(1)![]() (2)1.75;2 (3)见解析 (4)当
(2)1.75;2 (3)见解析 (4)当![]() 时,
时,![]() 随
随![]() 的增大而减小;当
的增大而减小;当![]() 时,
时,![]() 随
随![]() 的增大而增大.
的增大而增大.
【解析】
(1)根据题意,直接写出x的取值范围,即可;
(2)先证BAD~CDE,可得![]() ,进而得y关于x的解析式,分别求出当x=3时,当x=4时,y的值,即可;
,进而得y关于x的解析式,分别求出当x=3时,当x=4时,y的值,即可;
(3)根据函数解析式或表格中的数据与自变量的取值范围,画出函数图象,即可;
(4)根据二次函数的性质,即可得到答案.
(1)∵点![]() 是
是![]() 边上的一个动点(不与
边上的一个动点(不与![]() ,
,![]() 重合),
重合),![]() ,
,
∴![]() ,
,
故答案是:![]() ;
;
(2)∵∠B+∠BAD=∠ADE+∠CDE,![]() ,
,
∴∠BAD=∠CDE,
∵![]() ,
,
∴∠B=∠C,
∴BAD~CDE,
∴![]() ,即:
,即:![]() ,
,
∴![]() ,
,
∴当x=3时,y=1.75;当x=4时,y=2,
故答案是:1.75,2;
(3)函数图象如下:
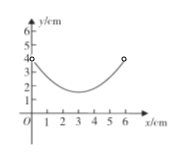
(4)由函数的图象和性质可知:当![]() 时,
时,![]() 随
随![]() 的增大而减小;当
的增大而减小;当![]() 时,
时,![]() 随
随![]() 的增大而增大.
的增大而增大.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形ABCD的对角线BD经过坐标原点O,矩形的边分别平行于坐标轴,点A在函数![]() (
(![]() ≠0,
≠0,![]() <0)的图象上,点C的坐标为(2,
<0)的图象上,点C的坐标为(2,![]() ),则
),则![]() 的值为( )
的值为( )
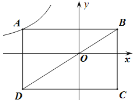
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点B、C,经过B、C两点的抛物线
轴分别相交于点B、C,经过B、C两点的抛物线![]() 与
与![]() 轴的另一个交点为A,顶点为P,且对称轴为直线
轴的另一个交点为A,顶点为P,且对称轴为直线![]() 。点G是抛物线
。点G是抛物线![]() 位于直线
位于直线![]() 下方的任意一点,连接PB、GB、GC、AC .
下方的任意一点,连接PB、GB、GC、AC .
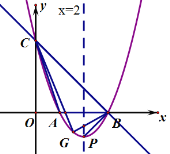
(1)求该抛物线的解析式;
(2)求△GBC面积的最大值;
(3)连接AC,在![]() 轴上是否存在一点Q,使得以点P,B,Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由。
轴上是否存在一点Q,使得以点P,B,Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC,顶点B(0,0),C(2,0),规定把△ABC先沿x轴绕着点C顺时针旋转,使点A落在x轴上 ,称为一次变换,再沿x轴绕着点A顺时针旋转,使点B落在x轴上 ,称为二次变换,……经过连续2017次变换后,顶点A的坐标是:

A. (4033, ![]() ) B. (4033,0) C. (4036,
) B. (4033,0) C. (4036, ![]() ) D. (4036,0)
) D. (4036,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, AB 是 ⊙ O 的直径, C 是![]() 的中点, CE ⊥ AB 于 E , BD 交 CE 于 F .
的中点, CE ⊥ AB 于 E , BD 交 CE 于 F .
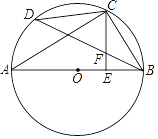
(1)求证: CF=BF ;
(2)若 CD=6 ,AC=8 ,求 BE 、 CF 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.如图,5×5正方形方格纸图中,点A,B都在格点处.
(1)请在图中作等腰△ABC,使其底边AC=2![]() ,且点C为格点;
,且点C为格点;
(2)在(1)的条件下,作出平行四边形ABDC,且D为格点,并直接写出平行四边形ABDC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】寒假中,某校七年级开展“阅读经典,读一本好书”的活动.为了解学生阅读情况,从全年级学生中随机抽取了部分学生调查读书种类情况,并进行统计分析,绘制了如下不完整的统计图表:
读书种类情况统计表
种类 | 频数 | 百分比 |
A.科普类 | a | 32% |
B.文学类 | 20 | 40% |
C.艺术类 | 8 | b |
D.其他类 | 6 | 12% |
请根据以上信息,解答下列问题:
(1)填空:a= ,b= ,并补全条形统计图;
(2)若绘制“阅读情况扇形统计图”,则“艺术类”所对应扇形的圆心角度数为 °;
(3)若该校七年级共有800人,请估计全年级在本次活动中读书种类为“艺术类”的学生人数.
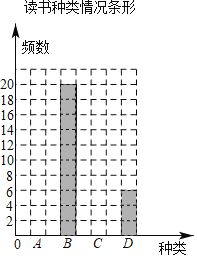
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线AC、BD交于点O,已知O是AC的中点,AE=CF,DF∥BE.
(1)求证:△BOE≌△DOF;
(2)若OD=OC,则四边形ABCD是什么特殊四边形?请直接给出你的结论,不必证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com