
ЁОЬтФПЁПШчЭМЃЈ1ЃЉЃЌдкдЅЮїФЯЕЫжнЪаДѓЪЎзжНжЮїФЯЗНЃЌЫЪСЂзХвЛзљЙХРЯНЈжў-ИЃЪЄЫТшѓЫўЃЌНЈгкББЫЮЬьЪЅЪЎФъЃЈЙЋдЊ1032ФъЃЉЃЌбЇЭъСЫШ§НЧКЏЪ§жЊЪЖКѓЃЌФГаЃЁАЪ§бЇЩчЭХЁБЕФСѕУїКЭЭѕЛЊОіЖЈгУздМКбЇЕНЕФжЊЪЖВтСПЁАИЃЪЄЫТшѓЫўЁБЕФИпЖШЃЎШчЭМЃЈ2ЃЉЃЌСѕУїдкЕуCДІВтЕУЫўЖЅBЕФбіНЧЮЊ45ЁуЃЌЭѕЛЊдкИпЬЈЩЯЕФЕуDДІВтЕУЫўЖЅBЕФбіНЧЮЊ40ЁуЃЌШєИпЬЈDEИпЮЊ5УзЃЌЕуDЕНЕуCЕФЫЎЦНОрРыECЮЊ1.3УзЃЌЧвAЁЂCЁЂEШ§ЕуЙВЯпЃЌЧѓИУЫўABЕФИпЖШЃЎЃЈВЮПМЪ§ОнЃКsin40ЁуЁж0.64ЃЌcos40ЁуЁж0.77ЃЌtan40ЁуЁж0.84ЃЌНсЙћБЃСєећЪ§ЃЉ

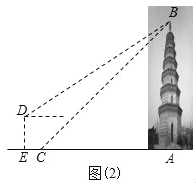
ЁОД№АИЁП38Уз
ЁОНтЮіЁП
зїDMЁЭABгкMЃЌНЛCBгкFЃЌCGЁЭDMгкGЃЌИљОнОиаЮЕФаджЪЕУЕНCG=DE=5ЃЌDG=EC=1.3ЃЌЩшFM=xУзЃЌИљОне§ЧаЕФЖЈвхгУxБэЪОГіDMЁЂBMЃЌНсКЯЭМаЮСаГіЗНГЬЃЌНтЗНГЬЕУЕНД№АИЃЎ
НтЃКШчЭМЃЌзїDMЁЭABгкMЃЌНЛCBгкFЃЌCGЁЭDMгкGЃЌдђЫФБпаЮDECGЮЊОиаЮЃЌ
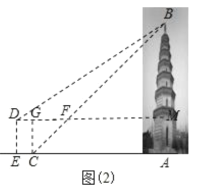
ЁрCGЃНDEЃН5ЃЌDGЃНECЃН1.3ЃЌ
ЩшFMЃНxУзЃЌгЩЬтвтЕУЃЌЁЯBDMЃН40ЁуЃЌЁЯBFMЃНЁЯBCAЃН45ЁуЃЌ
ЁрЁЯCFGЃН45ЁуЃЌBMЃНFMЃНxЃЌ
ЁрGFЃНGCЃН5ЃЌ
ЁрDFЃНDG+GFЃН5+1.3ЃН6.3ЃЌ
дкRtЁїBDMжаЃЌtanЁЯBDMЃН![]() ЃЌ
ЃЌ
ЁрDMЃН![]() ЃЌ
ЃЌ
гЩЬтвтЕУЃЌDMЉDFЃНFMЃЌМД![]() ЃЌ
ЃЌ
НтЕУЃЌxЁж33.2ЃЌдђBAЃНBM+AMЃН38.2Ёж38ЃЈУзЃЉЃЌ
Д№ЃКИУЫўABЕФИпЖШдМЮЊ38УзЃЎ


 аТПЮБъЭЌВНбЕСЗЯЕСаД№АИ
аТПЮБъЭЌВНбЕСЗЯЕСаД№АИ вЛЯпУћЪІПкЫугІгУЬтЬьЬьСЗвЛБОШЋЯЕСаД№АИ
вЛЯпУћЪІПкЫугІгУЬтЬьЬьСЗвЛБОШЋЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
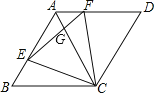
ЁОЬтФПЁПШчЭМЃЌСтаЮABCDЕФБпГЄЮЊ4ЃЌEЃЌFЗжБ№ЪЧABЃЌADБпЩЯЕФЖЏЕуЃЌBEЃНAFЃЌЁЯBADЃН120ЁуЃЌдђЯТСаНсТлЃКЂйЁїBECЁеЁїAFCЃЛЂкЁїECFЮЊЕШБпШ§НЧаЮЃЛЂлЁЯAGEЃНЁЯAFCЃЛЂмШєAFЃН1ЃЌдђ![]() ЃЎ Цфжае§ШЗНсТлЕФађКХга________ЃЎ
ЃЎ Цфжае§ШЗНсТлЕФађКХга________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЗДБШР§КЏЪ§![]() ЕФЭМЯѓОЙ§Еу
ЕФЭМЯѓОЙ§Еу![]() ЃЌЙ§
ЃЌЙ§![]() зї
зї![]() жсгкЕу
жсгкЕу![]() ЃЎЕу
ЃЎЕу![]() ЮЊЗДБШР§КЏЪ§ЭМЯѓЩЯЕФвЛЖЏЕуЃЌЙ§Еу
ЮЊЗДБШР§КЏЪ§ЭМЯѓЩЯЕФвЛЖЏЕуЃЌЙ§Еу![]() зї
зї![]() жсгкЕу
жсгкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎжБЯп
ЃЎжБЯп![]() гы
гы![]() жсЕФИКАыжсНЛгкЕу
жсЕФИКАыжсНЛгкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФУцЛ§ЃЛ
ЕФУцЛ§ЃЛ
ЃЈ3ЃЉЪЧЗёДцдкЕу![]() ЃЌЪЙЕУЫФБпаЮ
ЃЌЪЙЕУЫФБпаЮ![]() ЮЊЦНааЫФБпаЮЃПШєДцдкЃЌЧыЧѓГіЕу
ЮЊЦНааЫФБпаЮЃПШєДцдкЃЌЧыЧѓГіЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯп![]() гы
гы![]() жсЁЂ
жсЁЂ![]() жсЗжБ№ЯрНЛгкЕуBЁЂCЃЌОЙ§BЁЂCСНЕуЕФХзЮяЯп
жсЗжБ№ЯрНЛгкЕуBЁЂCЃЌОЙ§BЁЂCСНЕуЕФХзЮяЯп![]() гы
гы![]() жсЕФСэвЛИіНЛЕуЮЊAЃЌЖЅЕуЮЊPЃЌЧвЖдГЦжсЮЊжБЯп
жсЕФСэвЛИіНЛЕуЮЊAЃЌЖЅЕуЮЊPЃЌЧвЖдГЦжсЮЊжБЯп![]() ЁЃЕуGЪЧХзЮяЯп
ЁЃЕуGЪЧХзЮяЯп![]() ЮЛгкжБЯп
ЮЛгкжБЯп![]() ЯТЗНЕФШЮвтвЛЕуЃЌСЌНгPBЁЂGBЁЂGCЁЂAC .
ЯТЗНЕФШЮвтвЛЕуЃЌСЌНгPBЁЂGBЁЂGCЁЂAC .
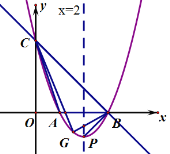
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓЁїGBCУцЛ§ЕФзюДѓжЕЃЛ
ЃЈ3ЃЉСЌНгACЃЌдк![]() жсЩЯЪЧЗёДцдквЛЕуQЃЌЪЙЕУвдЕуPЃЌBЃЌQЮЊЖЅЕуЕФШ§НЧаЮгыЁїABCЯрЫЦЃПШєДцдкЃЌЧѓГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЁЃ
жсЩЯЪЧЗёДцдквЛЕуQЃЌЪЙЕУвдЕуPЃЌBЃЌQЮЊЖЅЕуЕФШ§НЧаЮгыЁїABCЯрЫЦЃПШєДцдкЃЌЧѓГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСВФСЯЃК
ВФСЯвЛЃКЖдЪЕЪ§aЁЂbЃЌЖЈвх![]() ЕФКЌвхЮЊЃКЕБ
ЕФКЌвхЮЊЃКЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛЕБ
ЃЛЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЎР§ШчЃК
ЃЎР§ШчЃК![]() ЃЛ
ЃЛ![]() ЃЎ
ЃЎ
ВФСЯЖўЃКЙигкЪ§бЇМвИпЫЙЕФЙЪЪТЃЌ200ЖрФъЧАЃЌИпЫЙЕФЫуЪѕРЯЪІЬсГіСЫЯТУцЕФЮЪЃК![]() ОнЫЕЃЌЕБЦфЫћЭЌбЇУІгкАб100ИіЪ§ж№ЯюЯрМгЪБЃЌЪЎЫъЕФИпЫЙШДгУЯТУцЕФЗНЗЈбИЫйЫуГіСЫе§ШЗД№АИЃК
ОнЫЕЃЌЕБЦфЫћЭЌбЇУІгкАб100ИіЪ§ж№ЯюЯрМгЪБЃЌЪЎЫъЕФИпЫЙШДгУЯТУцЕФЗНЗЈбИЫйЫуГіСЫе§ШЗД№АИЃК![]() ЃЎвВПЩвдетбљРэНтЃКСю
ЃЎвВПЩвдетбљРэНтЃКСю![]() ЂйЃЌдђ
ЂйЃЌдђ![]() ЂкЃЌЂй+ЂкЃК
ЂкЃЌЂй+ЂкЃК![]() ЃЌМД
ЃЌМД![]() ЃЎ
ЃЎ
ИљОнвдЩЯВФСЯЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉвбжЊ![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉвбжЊ![]() ЃЌЧв
ЃЌЧв![]() ЃЌЛЏМђЃК
ЃЌЛЏМђЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЖдгке§Ъ§mЃЌга![]() ЃЌЧѓ
ЃЌЧѓ![]() Ё+
Ё+![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
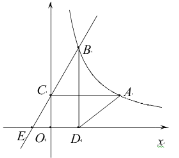
ЁОЬтФПЁПвбжЊЕШБпЁїABCЃЌЖЅЕуB(0,0),C(2,0),ЙцЖЈАбЁїABCЯШбиxжсШЦзХЕуCЫГЪБеыа§зЊЃЌЪЙЕуAТфдкxжсЩЯ ЃЌГЦЮЊвЛДЮБфЛЛЃЌдйбиxжсШЦзХЕуAЫГЪБеыа§зЊЃЌЪЙЕуBТфдкxжсЩЯ ЃЌГЦЮЊЖўДЮБфЛЛЃЌЁЁОЙ§СЌај2017ДЮБфЛЛКѓЃЌЖЅЕуAЕФзјБъЪЧЃК

A. (4033ЃЌ ![]() ) B. (4033ЃЌ0) C. (4036ЃЌ
) B. (4033ЃЌ0) C. (4036ЃЌ ![]() ) D. (4036ЃЌ0)
) D. (4036ЃЌ0)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ AB ЪЧ Ёб O ЕФжБОЖЃЌ C ЪЧ![]() ЕФжаЕуЃЌ CE ЁЭ AB гк E ЃЌ BD НЛ CE гк F ЃЎ
ЕФжаЕуЃЌ CE ЁЭ AB гк E ЃЌ BD НЛ CE гк F ЃЎ
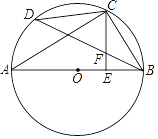
ЃЈ1ЃЉЧѓжЄЃК CF=BF ЃЛ
ЃЈ2ЃЉШє CD=6 ЃЌAC=8 ЃЌЧѓ BE ЁЂ CF ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкУПИіаЁе§ЗНаЮЕФБпГЄЮЊ1ЕФЭјИёЭМаЮжаЃЌУПИіаЁе§ЗНаЮЕФЖЅЕуГЦЮЊИёЕу.ШчЭМЃЌ5ЁС5е§ЗНаЮЗНИёжНЭМжаЃЌЕуAЃЌBЖМдкИёЕуДІ.
(1)ЧыдкЭМжазїЕШбќЁїABCЃЌЪЙЦфЕзБпACЃН2![]() ЃЌЧвЕуCЮЊИёЕуЃЛ
ЃЌЧвЕуCЮЊИёЕуЃЛ
(2)дк(1)ЕФЬѕМўЯТЃЌзїГіЦНааЫФБпаЮABDCЃЌЧвDЮЊИёЕуЃЌВЂжБНгаДГіЦНааЫФБпаЮABDCЕФУцЛ§.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2018ФъЃЌЙњМвЮРЩњНЁПЕЮЏдБЛсКЭЙњМвНЬг§ВПдкШЋЙњПЊеЙСЫЖљЭЏЧрЩйФъНќЪгЕїВщЙЄзїЃЌЕїВщЪ§ОнЯдЪОЃЌШЋЙњЖљЭЏЧрЩйФъНќЪгЙ§АыЃЎФГаЃГѕШ§бЇЯАаЁзщЮЊСЫНтБОаЃбЇЩњЖдздМКЪгСІБЃЛЄЕФжиЪгГЬЖШЃЌЫцЛњдкаЃФкЕїВщСЫВПЗжбЇЩњЃЌЕїВщНсЙћЗжЮЊЁАЗЧГЃжиЪгЁБЁАжиЪгЁБЁАБШНЯжиЪгЁБЁАВЛжиЪгЁБЫФРрЃЌВЂНЋНсЙћЛцжЦГЩЯТУцЕФСНЗљВЛЭъећЕФЭГМЦЭМЃК
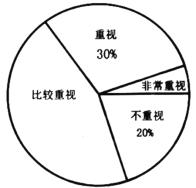
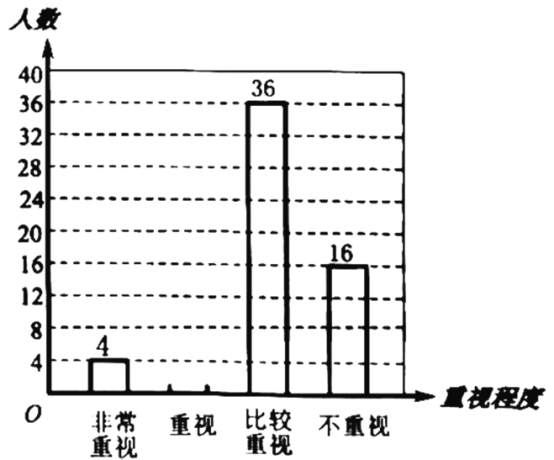
ИљОнЭМжааХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧѓБОДЮЕїВщЕФбЇЩњзмШЫЪ§ЃЌВЂВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉИУаЃЙВгабЇЩњ1000ШЫЃЌЧыФуЙРМЦИУаЃЖдЪгСІБЃЛЄЁАЗЧГЃжиЪгЁБЕФбЇЩњШЫЪ§ЃЛ
ЃЈ3ЃЉЖдЪгСІЁАЗЧГЃжиЪгЁБЕФ4ШЫга![]() ЃЌ
ЃЌ![]() СНУћФаЩњЃЌ
СНУћФаЩњЃЌ![]() ЃЌ
ЃЌ![]() СНУћХЎЩњЃЌШєДгжаЫцЛњГщШЁСНШЫЯђШЋаЃзїЪгСІБЃЛЄНЛСїЃЌЧыРћгУЪїзДЭМЛђСаБэЕФЗНЗЈЃЌЧѓЧЁКУГщЕНвЛФавЛХЎЕФИХТЪЃЎ
СНУћХЎЩњЃЌШєДгжаЫцЛњГщШЁСНШЫЯђШЋаЃзїЪгСІБЃЛЄНЛСїЃЌЧыРћгУЪїзДЭМЛђСаБэЕФЗНЗЈЃЌЧѓЧЁКУГщЕНвЛФавЛХЎЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com