
【题目】阅读材料:
材料一:对实数a、b,定义![]() 的含义为:当
的含义为:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .例如:
.例如:![]() ;
;![]() .
.
材料二:关于数学家高斯的故事,200多年前,高斯的算术老师提出了下面的问:![]() 据说,当其他同学忙于把100个数逐项相加时,十岁的高斯却用下面的方法迅速算出了正确答案:
据说,当其他同学忙于把100个数逐项相加时,十岁的高斯却用下面的方法迅速算出了正确答案:![]() .也可以这样理解:令
.也可以这样理解:令![]() ①,则
①,则![]() ②,①+②:
②,①+②:![]() ,即
,即![]() .
.
根据以上材料,回答下列问题:
(1)已知![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(2)已知![]() ,且
,且![]() ,化简:
,化简:![]() ;
;
(3)对于正数m,有![]() ,求
,求![]() …+
…+![]() 的值.
的值.
科目:初中数学 来源: 题型:
【题目】近些年全国各地频发雾霾天气,给人民群众的身体健康带来了危害,某商场看到商机后决定购进甲、乙两种空气净化器进行销售.若每台甲种空气净化器的进价比每台乙种空气净化器的进价少300元,且用6000元购进甲种空气净化器的数量与用7500元购进乙种空气净化器的数量相同.
(1)求每台甲种空气净化器、每台乙种空气净化器的进价分别为多少元?
(2)若该商场准备进货甲、乙两种空气净化器共30台,且进货花费不超过42000元,问最少进货甲种空气净化器多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )

A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
科目:初中数学 来源: 题型:
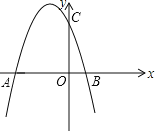
【题目】如图,抛物线y=ax2+bx+3与x轴交于A(﹣3,0),B(l,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)点P是抛物线上的动点,且满足S△PAO=2S△PCO,求出P点的坐标;
(3)连接BC,点E是x轴一动点,点F是抛物线上一动点,若以B、C、E、F为顶点的四边形是平行四边形时,请直接写出点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了开展“阳光体育运动”,计划购买篮球和足球.已知购买20个篮球和40个足球的总金额为4600元;购买30个篮球和50个足球的总金额为6100元.
(1)每个篮球、每个足球的价格分别为多少元?
(2)若该校购买篮球和足球共60个,且购买篮球的总金额不超过购买足球的总金额,则该校最多可购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
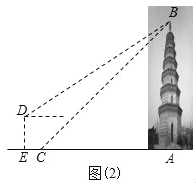
【题目】如图(1),在豫西南邓州市大十字街西南方,耸立着一座古老建筑-福胜寺梵塔,建于北宋天圣十年(公元1032年),学完了三角函数知识后,某校“数学社团”的刘明和王华决定用自己学到的知识测量“福胜寺梵塔”的高度.如图(2),刘明在点C处测得塔顶B的仰角为45°,王华在高台上的点D处测得塔顶B的仰角为40°,若高台DE高为5米,点D到点C的水平距离EC为1.3米,且A、C、E三点共线,求该塔AB的高度.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
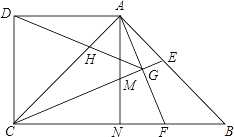
【题目】如图,在四边形 ABCD 中,AD ∥ BC ,∠BCD=90° ,∠ABC=45° ,AD=CD ,CE 平分 ∠ ACB 交 AB 于点 E ,在 BC 上截取 BF=AE ,连接 AF 交 CE 于点 G ,连接 DG 交 AC 于点 H ,过点 A 作 AN ⊥ BC ,垂足为 N , AN 交 CE 于点 M .则下列结论:① CM=AF ; ② CE ⊥ AF ; ③△ ABF ∽△ DAH ;④ GD 平分 ∠ AGC ,其中正确的序号是 ________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( )

A. π B. ![]() C. 3+π D. 8﹣π
C. 3+π D. 8﹣π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)中的x与y的部分对应值如表所示,则下列结论中,正确的个数有( )
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
①a<0;②当x<0时,y<3;③当x>1时,y的值随x值的增大而减小;④方程ax2+bx+c=5有两个不相等的实数根.
A.4个B.3个C.2个D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com