
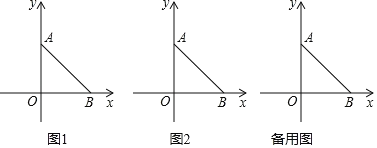
����Ŀ����֪����ͼ��ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬A��B�ֱ���y���������x���������ϵĵ㣬OA=OB=a��a�����ʽ2a��2��16=64��
��1�����A�����ꣻ
��2������C��O�������x�Ḻ���᷽���ȶ����ٶ�Ϊÿ��2����λ���ȣ�����B��BD��AC��D����y���ڵ�E����C���˶�ʱ��Ϊt���ú�t�Ĵ���ʽ��ʾ�߶�AE�ij���
��3���ڣ�2���������¹���O��OF��BD�ڵ�F����AB�ڵ�G������EG���Ƿ����tֵ��ʹ��AGE=��OGB�����������tֵ����������˵�����ɣ�
���𰸡���1��A��0��4������2��AE=4��2t����3��t=1��
��������
��1����ͬ�����ݵij˷�����a��ֵ��
��2���ɡ�AAS����֤��ACO�ա�BEO���ɵ�CO��OE��2t��������AE�ij���
��3������A��AH��OB����OG�ӳ�����H���ɡ�ASA����֤��AGE�ա�AGH���ɵ�AH��AE��4��2t���ɡ�ASA����֤��AOH�ա�OBE���ɵ�AH��OE��������t��ֵ��
��1����2a��2��16=64��
��a��2=2��
��a=4��
��OA=OB=a��
��OA=OB=4��
���A��0��4������B��4��0����
��2����ͼ1��
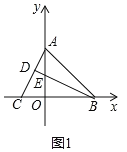
��BD��AC��AO��BC��
���ACO+��CBD=90![]() ����ACO+��CAO=90
����ACO+��CAO=90![]() ��
��
���CBD=��CAO����AO=BO����AOC=��BOE=90![]() ��
��
���ACO�ա�BEO��AAS����
��CO=OE=2t��
��AE=AO��OE=4��2t��
��3������.
��ͼ2������A��AH��OB����OG�ӳ�����H��
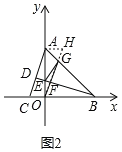
���HAO=��AOB=90![]() ��
��
��AO=BO����AOB=90![]() ��
��
���OAB=��OBA=45![]() ��
��
���HAG=��OAB=45![]() ����AG=AG����AGE=��OGB=��AGH��
����AG=AG����AGE=��OGB=��AGH��
���AGE�ա�AGH��ASA����
��AH=AE=4��2t��
��OF��BD��
���FOB+��OBD=90![]() ���ҡ�AOH+��FOB=90
���ҡ�AOH+��FOB=90![]() ��
��
���AOH=��OBD����AO=OB����HAO=��EOB��
���AOH�ա�OBE��ASA����
��AH=OE��
��4��2t=2t��
��t=1��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
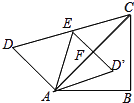
����Ŀ����ͼ����һ��ֱ�����ǰ�ƴ��һ����ı���ABCD����ACB=45�㣬��ACD=30������EΪCD���ϵ��е㣬����AE������ADE��AE����ֱ�߷��۵õ���AD��E��D��E��AC��F�㣬��AB= 6![]() cm����D����BC�ľ����ǣ� ��
cm����D����BC�ľ����ǣ� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����װ�깺��һ�����£��۸�Ϊÿ��30Ԫ����۲��Ź涨�����۵��۲�����ÿ��70Ԫ�����г����鷢�֣���������y�����������۵���x��Ԫ����һ�κ������ҵ�x=60ʱ��y=80��x=50ʱ��y=100�������۹����У�ÿ�컹Ҫ֧����������450Ԫ��
��1�����y��x�ĺ�����ϵʽ��
��2����÷�װ��Ҫ���������������ջ���750Ԫ���ۼ�Ӧ������Ԫ��
��3�������۵���Ϊ����Ԫʱ���÷�װ���ջ�������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �ǵȱ������Σ���
�ǵȱ������Σ���![]() Ϊ
Ϊ![]() ����һ�㣬��
����һ�㣬��![]() Ϊ�����ȱ�
Ϊ�����ȱ�![]() ������
������![]() ����
����![]() ��
��![]() ����
����![]() �� ��
�� ��

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ���Ե�
���Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() ��Ϊ�뾶������������
��Ϊ�뾶������������![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ������
������![]() ����
����![]() ����
����![]() ������Ϊ
������Ϊ![]() ��
��

��1���߶�![]() ��ͼ�����е���һ���߶���ȣ���ó��Ľ����ǣ�
��ͼ�����е���һ���߶���ȣ���ó��Ľ����ǣ�![]() ��
��
��2��֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������12�֣�
��֪����Rt��ABC��Rt��DEF����ͼ��1���ڷţ���C���E�غϣ�����B��C��E����F��ͬһ��ֱ���ϣ���ACB = ��EDF = 90�㣬��DEF = 45����AC = 8 cm��BC = 6 cm��EF = 9 cm��
��ͼ��2������DEF��ͼ��1����λ�ó�������1 cm/s���ٶ���CB����ABC��������������DEF������ͬʱ����P����ABC�Ķ���B��������2 cm/s���ٶ���BA���A��������.����DEF�Ķ���D�ƶ���AC����ʱ����DEFֹͣ��������PҲ��ֹ֮ͣ�ƶ���DE��AC�ཻ�ڵ�Q������PQ��������ʱ��Ϊt��s����0��t��4.5����

����������⣺
��1����tΪ��ֵʱ����A���߶�PQ�Ĵ�ֱƽ�����ϣ�
��2������PE�����ı���APEC�����Ϊy��cm2������y��t֮��ĺ�����ϵʽ���Ƿ����ijһʱ��t��ʹ���y��С�������ڣ����y����Сֵ���������ڣ�˵�����ɣ�
��3���Ƿ����ijһʱ��t��ʹP��Q��F������ͬһ��ֱ���ϣ������ڣ������ʱt��ֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
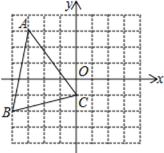
����Ŀ����ͼ�������д�������ϵ�������У���ABC�Ķ��㶼�ڱ߳�Ϊ1��С�����εĶ�����
(1) ֱ��д�����꣺A__________��B__________
(2) ������ABC����y��ĶԳƵ���DEC����D���A��Ӧ��
(3) ���̶ȵ�ֱ�ߣ�����ȫ�ȵ�֪ʶ������ABC�ĸ���BF��������ͼ�ۼ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
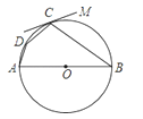
����Ŀ����ͼ���ı���ABCD�ڽ�����O��ABΪ��O��ֱ����CM����O�ڵ�C����BCM=60��������B������ֵ�ǣ�������
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���![]() +2x+2k��2=0����������ȵ�ʵ����.
+2x+2k��2=0����������ȵ�ʵ����.
��1����k��ȡֵ��Χ��
��2����kΪ����������÷��̵ĸ�.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com