
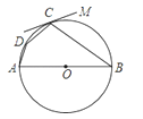
【题目】如图,四边形ABCD内接于⊙O,AB为⊙O的直径,CM切⊙O于点C,∠BCM=60°,则∠B的正切值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
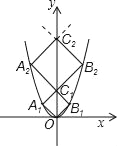
【题目】如图,已知点A1、A2、…A2018在函数y=2x2位于第二象限的图象上,点B1、B2,…,B2018在函数y=2x2位于第一象限的图象上,点C1,C2,…,C2018在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2017A2018C2018B2018都是正方形,则正方形C2017A2018C2018B2018的边长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
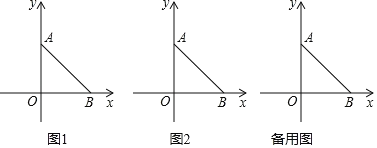
【题目】已知:如图在平面直角坐标系中,O为坐标原点,A、B分别是y轴正半轴和x轴正半轴上的点,OA=OB=a,a满足等式2a﹣2×16=64.
(1)求点A的坐标;
(2)动点C从O点出发沿x轴负半轴方向匀动,速度为每秒2个单位长度,过点B作BD⊥AC于D,交y轴于点E,设C的运动时间为t,用含t的代数式表示线段AE的长.
(3)在(2)的条件下过点O作OF⊥BD于点F,交AB于点G,连接EG,是否存在t值,使∠AGE=∠OGB,若存在求出t值,若不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
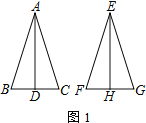
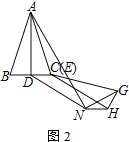
【题目】如图1,AB=AC,EF=EG,△ABC≌△EFG,AD⊥BC于点D,EH⊥FG于点H
(1) 直接写出AD、EH的数量关系:___________________
(2) 将△EFG沿EH剪开,让点E和点C重合
① 按图2放置△EHG,将线段CD沿EH平移至HN,连接AN、GN,求证:AN⊥GN
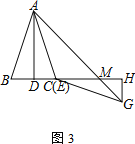
② 按图3放置△EHG,B、C(E)、H三点共线,连接AG交EH于点M.若BD=1,AD=3,求CM的长度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年某市水果大丰收,![]() 两个水果基地分别收获同种水果
两个水果基地分别收获同种水果![]() 件、
件、![]() 件,现需把这些水果全部运往甲、乙两销售点,从
件,现需把这些水果全部运往甲、乙两销售点,从![]() 基地运往甲、乙两销售点的费用分别为每件
基地运往甲、乙两销售点的费用分别为每件![]() 元和
元和![]() 元,从
元,从![]() 基地运往甲、乙两销售点的费用分别为每件
基地运往甲、乙两销售点的费用分别为每件![]() 元和
元和![]() 元,现甲销售点需要水果
元,现甲销售点需要水果![]() 件,乙销售点需要水果
件,乙销售点需要水果![]() 件.
件.
![]() 设从
设从![]() 基地运往甲销售点水果
基地运往甲销售点水果![]() 件,总运费为
件,总运费为![]() 元,请用含的
元,请用含的![]() 代数式表示
代数式表示![]() ,并写出
,并写出![]() 的取值范围;
的取值范围;
![]() 若总运费不超过
若总运费不超过![]() 元,且
元,且![]() 基地运往甲销售点的水果不低于
基地运往甲销售点的水果不低于![]() 件,试确定运费最低的运输方案,并求出最低运费.
件,试确定运费最低的运输方案,并求出最低运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,
,![]() ,已知点
,已知点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是该直线上的一个动点.
是该直线上的一个动点.
(1)![]() ________;
________;![]() 的坐标为__________;
的坐标为__________;
(2)若点![]() 在第二象限内运动,试写出
在第二象限内运动,试写出![]() 的面积
的面积![]() 关于
关于![]() 的函数解析式.
的函数解析式.
(3)探究:若点![]() 在该直线上任意运动,当
在该直线上任意运动,当![]() 的面积为6时,点
的面积为6时,点![]() 的坐标为________.
的坐标为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用火柴棒摆-列正方形图案,第①个图案用了4根,第②个图案用了12根,第③个图案用了24根,按照此规律,摆出第⑦个图案用火柴棒的根数是( )
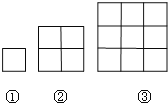
A.110B.112C.114D.116
查看答案和解析>>
科目:初中数学 来源: 题型:
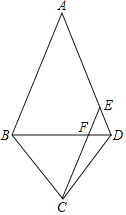
【题目】如图,在四边形ABCD中,AB=AD,BC=DC,点E为AD边上一点,连接BD、CE,CE与BD交于点F,且CE∥AB,若AB=8,CE=6,若△FCD的面积为2![]() ,则四边形ABCD的面积为_____.
,则四边形ABCD的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为![]() (m2),种草所需费用
(m2),种草所需费用![]() 1(元)与
1(元)与![]() (m2)的函数关系式为
(m2)的函数关系式为 ,其图象如图所示:栽花所需费用
,其图象如图所示:栽花所需费用![]() 2(元)与x(m2)的函数关系式为
2(元)与x(m2)的函数关系式为![]() 2=﹣0.01
2=﹣0.01![]() 2﹣20
2﹣20![]() +30000(0≤
+30000(0≤![]() ≤1000).
≤1000).

(1)请直接写出k1、k2和b的值;
(2)设这块1000m2空地的绿化总费用为W(元),请利用W与![]() 的函数关系式,求出绿化总费用W的最大值;
的函数关系式,求出绿化总费用W的最大值;
(3)若种草部分的面积不少于700m2,栽花部分的面积不少于100m2,请求出绿化总费用W的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com