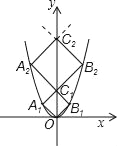
【题目】如图，已知点A1、A2、…A2018在函数y=2x2位于第二象限的图象上，点B1、B2，…，B2018在函数y=2x2位于第一象限的图象上，点C1，C2，…，C2018在y轴的正半轴上，若四边形OA1C1B1、C1A2C2B2，…，C2017A2018C2018B2018都是正方形，则正方形C2017A2018C2018B2018的边长是_____．
【答案】1009
【解析】
根据正方形对角线平分一组对角可得OB1与y轴的夹角为45°，然后表示出OB1的解析式，再与抛物线解析式联立求出点B1的坐标，然后求出OB1的长，再根据正方形的性质求出OC1，表示出C1B2的解析式，与抛物线联立求出B2的坐标，然后求出C1B2的长，再求出C1C2的长，然后表示出C2B3的解析式，与抛物线联立求出B3的坐标，然后求出C2B3的长，从而根据边长的变化规律解答即可．
解：∵OA1C1B1是正方形，
∴OB1与y轴的夹角为45°，
∴OB1的解析式为y=x，
联立方程组得：
，
解得 
，
．
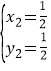∴B点的坐标是：（
，），
∴OB1=
=
=1×；
同理可得：正方形C1A2C2B2的边长C1B2=2×；
…
依此类推，正方形C2017A2018C2018B2018的边长是为2018×=1009．
故答案为1009．
科目：初中数学 来源： 题型：
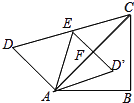
【题目】如图，将一副直角三角板拼在一起得四边形ABCD，∠ACB=45°，∠ACD=30°，点E为CD边上的中点，连接AE，将△ADE沿AE所在直线翻折得到△AD′E，D′E交AC于F点，若AB= 6
cm，点D′到BC的距离是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
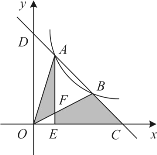
【题目】如图，一次函数 y＝－x＋b 与反比例函数y＝
(x＞0)的图象交于 A，B 两点，与 x 轴、y轴分别交于C，D 两点，连接 OA，OB，过 A 作 AE⊥x 轴于点 E，交 OB 于点F，设点 A 的横坐标为 m. 若 S△OAF＋S 四边形 EFBC＝4，则 m 的值是( )
A. 1 B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
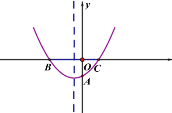
【题目】如图，二次函数y＝ax2＋bx＋c 的图象与 x 轴交于 B、C 两点，交 y 轴于点 A.
（1）根据图象请用“＞”、“＜”或“=”填空：a 0，b 0，c 0；
(2)如果 OC＝OA＝
OB，BC＝3，求这个二次函数的解析式;
(3) 在（2）中抛物线的对称轴上，存在点 Q 使得△OQA 的周长最短，试求出点 Q 的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线y=2x+3与x轴相交于点A，与y轴相交于点B.
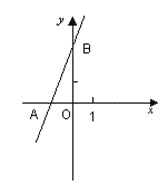
（1）求A，B两点的坐标；
（2）过B点作直线BP与x轴相交于P，且使OP=2OA， 求ΔABP的面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】服装店购进一批秋衣，价格为每件30元．物价部门规定其销售单价不高于每件70元，经市场调查发现：日销售量y（件）是销售单价x（元）的一次函数，且当x=60时，y=80；x=50时，y=100．在销售过程中，每天还要支付其他费用450元．
（1）求出y与x的函数关系式．
（2）求该服装店要想销售这批秋衣日获利750元，售价应定多少元？
（3）请销售单价为多少元时，该服装店日获利最大？最大获利是多少元？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
