
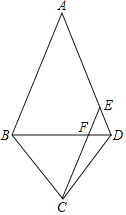
【题目】如图,在四边形ABCD中,AB=AD,BC=DC,点E为AD边上一点,连接BD、CE,CE与BD交于点F,且CE∥AB,若AB=8,CE=6,若△FCD的面积为2![]() ,则四边形ABCD的面积为_____.
,则四边形ABCD的面积为_____.
【答案】24![]()
【解析】
连接AC,证出AC垂直平分BD,由等腰三角形的性质得出∠ABD=∠ADB,∠BAC=∠DAC,由平行线的性质得出∠BAC=∠ACE,∠ABD=∠EFD,得出∠DAC=∠ACE,∠ADB=∠EFD,证出AE=CE=6,EF=DE=AD﹣AE=2,得出CF=CE﹣EF=4=2EF,得出△DEF的面积=![]() △FCD的面积=
△FCD的面积=![]() ,由平行线证明△EFD∽△ABD,得出
,由平行线证明△EFD∽△ABD,得出![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,求出S△ABD=16S△EFD=16
,求出S△ABD=16S△EFD=16![]() ,S△BCD=4S△FCD=8
,S△BCD=4S△FCD=8![]() ,即可得出答案.
,即可得出答案.
解:∵连接AC,如图所示:∵AB=AD=8,BC=DC,
∴AC垂直平分BD,∠ABD=∠ADB,
∴∠BAC=∠DAC,
∵CE∥AB,
∴∠BAC=∠ACE,∠ABD=∠EFD,
∴∠DAC=∠ACE,∠ADB=∠EFD,
∴AE=CE=6,EF=DE=AD﹣AE=2,
∴CF=CE﹣EF=4=2EF,
∵△FCD的面积为2![]() ,
,
∴△DEF的面积=![]() △FCD的面积=
△FCD的面积=![]() ,
,
∵CE∥AB,
∴△EFD∽△ABD,且![]() =
=![]() =
=![]() =
=![]() ,
,
∴![]() =(
=(![]() )2=
)2=![]() ,
,![]() =
=![]() =
=![]() ,
,
∴S△ABD=16S△EFD=16![]() ,S△BCD=4S△FCD=8
,S△BCD=4S△FCD=8![]() ,
,
∴四边形ABCD的面积=△ABD的面积+△BCD的面积=24![]() ;
;
故答案为:24![]() .
.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
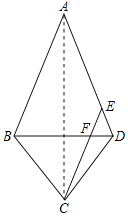
【题目】△ABC和△ECD都是等边三角形

(1)如图1,若B、C、D三点在一条直线上,求证:BE=AD;
(2)保持△ABC不动,将△ECD绕点C顺时针旋转,使∠ACE=90°(如图2),BC与DE有怎样的位置关系?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
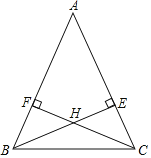
【题目】如图,AB=AC,BE与CF是△ABC的高线,且BE与CF相交于点H.
(1)求证:HB=HC;
(2)不添加辅助线,直接写出图中所有的全等三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
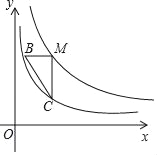
【题目】如图,点M在函数y=![]() (x>0)的图象上,过点M分别作x轴和y轴的平行线交函数y=
(x>0)的图象上,过点M分别作x轴和y轴的平行线交函数y=![]() (x>0)的图象于点B、C.
(x>0)的图象于点B、C.
(1)若点M的坐标为(1,3).
①求B、C两点的坐标;
②求直线BC的解析式;
(2)求△BMC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com