练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．如图，已知∠B=30°，∠D=20°，∠BCD=50°，那么AB∥DE吗？请说明理由．

    分析 先作CM∥AB，欲证明AB∥DE，只要证明CM∥DE即可．

    解答 解：AB∥DE．
    理由：如图，作CM∥AB，
    ∵CM∥AB，
    ∴∠B=∠BCM=30°，
    ∵∠BCD=50°，
    ∴∠MCD=50°-30°=20°，
    ∵∠D=20°，
    ∴∠D=∠MCD，
    ∴CM∥ED，
    ∴AB∥DE．

    点评 本题考查平行线的判定和性质，作出辅助线，运用平行线的判定和性质是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

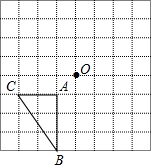    3．如图所示，△ABC的顶点与点O在8×8的网格中的格点上．
    （1）画出△ABC绕点O顺时针旋转90°得到的△A1B1C1；
    （2）画出△ABC绕点O逆时针旋转90°得到的△A2B2C2；
    （3）若⊙M能盖住△ABC，则⊙M的半径最小值为$\frac{\sqrt{13}}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．下列说法错误的是（　　）
    A．$\root{3}{{8}^{2}}$的平方根是±2B．$\root{3}{（x-1）^{3}}$的立方根是±（x-1）
    C．$\sqrt{（-3）^{2}}$的立方根是$\root{3}{3}$D．若$\sqrt{-x}$有意义，则$\sqrt{-x}$≥0

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．如图，△ABC中，∠C=90°，AM平分∠CAB，CM=20cm，那么M到AB的距离是（　　）
    A．15cmB．20cmC．25cmD．30cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．现有一个两位数，它的十位上的数比个位上的数的3倍小1，已知这个两位数的个位上的数是m，请根据如图所示的表示方式，完成下列各小题．
    （1）请用含m的整式表示出该两位数（结果要进行化简）
    （2）若把这个两位数的十位上的数和个位上的数对调．
    ①当m=3时，求得到的新的两位数是多少？
    ②求原来的两位数比得到的新的两位数大多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．计算下列各题
    （1）（-2.2）+3.8+0-（+1.6）
    （2）-7-（-11）+（-9）-（+2）
    （3）6$\frac{3}{5}$+23$\frac{6}{11}$-2$\frac{2}{15}$-18$\frac{6}{11}$
    （4）|-$\frac{3}{4}$|+$\frac{1}{6}$+（-$\frac{2}{3}$）-$\frac{5}{2}$
    （5）11+12-13-14+15+16-17-18+…+99+100．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

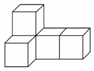    5．如图，它是由5个完全相同的小正方体搭建的几何体，若将最右边的小正方体拿走，则下列结论正确的是（　　）
    A．主视图不变B．左视图不变C．俯视图不变D．三视图都不变

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．一个不透明的盒子有有n个除颜色外其它完全相同的小球，其中有6个黄球，每次摸球前先将盒子里的球摇匀，任意摸出一个球记下颜色后在放回盒子，通过大量重复摸球实验后发现，摸到黄球的频率稳定在20%，那么可以推算出n大约是（　　）
    A．30B．20C．12D．6

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

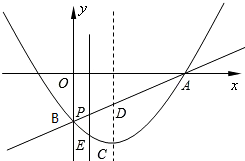    3． 如图，抛物线的顶点为C（1，-2），直线y=kx+m与抛物线交于A、B来两点，其中A点在x轴的正半轴上，且OA=3，B点在y轴上，点P为线段AB上的一个动点（点P与点A、B不重合），过点P且垂直于x轴的直线与这条抛物线交于点E．
    （1）求直线AB的解析式．
    （2）设点P的横坐标为x，求点E的坐标（用含x的代数式表示）．
    （3）求△ABE面积的最大值．

    查看答案和解析>>

    同步练习册答案