
【题目】如图,在平面直角坐标系中,直线y=2x+4与x轴交于点A,与y轴交于点B,过点B的直线交x轴于点C,且△ABC面积为10.
(1)求点C的坐标及直线BC的解析式;
(2)如图1,设点F为线段AB中点,点G为y轴上一动点,连接FG,以FG为边向FG右侧作长形FGQP,且FG:GQ=1:2,在G点的运动过程中,当顶点Q落在直线BC上时,求点G的坐标;
(3)如图2,若M为线段BC上一点,且满足S△AMB=S△AOB,点E为直线AM上一动点,在x轴上是存在点D,使以点D,E,B,C为顶点的四边形为平行四边形?若存在,请直接写出点D的坐标;若不在,请说明理由.

【答案】(1)C(3,0),y=﹣![]() x+4;(2)(
x+4;(2)(![]() ,
,![]() );(3)存在,点D的坐标为:(
);(3)存在,点D的坐标为:(![]() ,0)或(﹣
,0)或(﹣![]() ,0)或(﹣
,0)或(﹣![]() ,0).
,0).
【解析】
(1)直线y=2x+4与x轴交于点A,与y轴交于点B,则点A、B的坐标分别为:(﹣2,0)、(0,4),△ABC面积=![]() ×AC×OB=
×AC×OB=![]() AC×4=10,解得:AC=5,故点C(3,0),
AC×4=10,解得:AC=5,故点C(3,0),
将点B、C的坐标代入一次函数表达式,即可求解;
(2)证明△GNQ∽△FMG,则![]() ,即
,即![]() ,故点Q(2m﹣4,m﹣2),即可求解;
,故点Q(2m﹣4,m﹣2),即可求解;
(3)分BC是平行四边形的边、BC是平行四边形的对角线两种情况,分别求解即可.
解:(1)直线y=2x+4与x轴交于点A,与y轴交于点B,则点A、B的坐标分别为:(﹣2,0)、(0,4),
△ABC面积=![]() ×AC×OB=
×AC×OB=![]() AC×4=10,解得:AC=5,故点C(3,0),
AC×4=10,解得:AC=5,故点C(3,0),
将点B、C的坐标代入一次函数表达式并解得:
直线BC的表达式为:y=﹣![]() x+4…①;
x+4…①;
(2)设点E(m,![]() m+
m+![]() ),点D(n,0),点F为线段AB中点,则点F(﹣1,2),
),点D(n,0),点F为线段AB中点,则点F(﹣1,2),
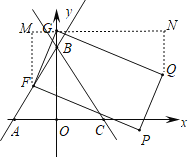
过点G作x轴的平行线MN,过点F、Q分别作y轴的平行线分别交MN于点M、N,
∵∠MGF+∠GFM=90°,∠MGF+∠NGQ=90°,∴∠NGQ=∠GFM,
∠GNQ=∠FMG=90°,
∴△GNQ∽△FMG,
∴![]() ,即
,即![]() ,
,
故:GN=2m﹣4,QN=2,故点Q(2m﹣4,m﹣2),
将点Q的坐标代入y=﹣![]() x+4并解得:m=
x+4并解得:m=![]() ,
,
故点Q(![]() ,
,![]() );
);
(3)S△AMB=S△AOB,则OM∥AB,
则直线OM的表达式为:y=2x…②,
联立①②并解得:x=![]() ,故点M(
,故点M(![]() ,
,![]() ),
),
同理直线AM的表达式为:y=![]() x+
x+![]() ,
,
设点E(m,![]() m+
m+![]() ),点D(n,0),
),点D(n,0),
①当BC是平行四边形的边时,
点B向右平移3个单位向下平移4个单位得到C,
同样点E(D)向右平移3个单位向下平移4个单位得到D(E),
则m+3=n,![]() m+
m+![]() ﹣4=0或m﹣3=n,
﹣4=0或m﹣3=n,![]() m+
m+![]() +4=0,
+4=0,
解得:n=![]() 或n=﹣
或n=﹣![]() ;
;
②当BC是平行四边形的对角线时,
由中点公式得:m+n=3,![]() m+
m+![]() +4=0,
+4=0,
解得:n=﹣![]() ,
,
故点D的坐标为:(![]() ,0)或(﹣
,0)或(﹣![]() ,0)或(﹣
,0)或(﹣![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】如图,在离水面高度(AC)为2米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米的速度收绳子.
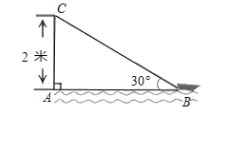
问:(1)未开始收绳子的时候,图中绳子BC的长度是多少米?
(2)收绳2秒后船离岸边多少米?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
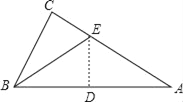
【题目】有一直角三角形纸片,∠C=90°,BC=6,AC=8,现将△ABC按如图那样折叠,使点A与点B重合,折痕为DE,则CE的长为( )
A. 2![]() B.
B. ![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l:y=kx和抛物线C:y=ax2+bx+1.
(1)当k=1,b=1时,抛物线C:y=ax2+bx+1的顶点在直线l:y=kx上,求a的值;
(2)若把直线l向上平移k2+1个单位长度得到直线r,则无论非零实数k取何值,直线r与抛物线C都只有一个交点;
(i)求此抛物线的解析式;
(ii)若P是此抛物线上任一点,过点P作PQ∥y轴且与直线y=2交于点Q,O为原点,
求证:OP=PQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂以每千克200元的价格购进甲种原料360千克,用于生产A、B两种产品,生产1件A产品或1件B产品所需甲、乙两种原料的千克数如下表:
产品/原料 | A | B |
甲(千克) | 9 | 4 |
乙(千克) | 3 | 10 |
乙种原料的价格为每千克300元,A产品每件售价3000元,B产品每件售价4200元,现将甲种原料全部用完,设生产A产品x件,B产品m件,公司获得的总利润为y元.
(1)写出m与x的关系式;
(2)求y与x的关系式;
(3)若使用乙种原料不超过510千克,生产A种产品多少件时,公司获利最大?最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
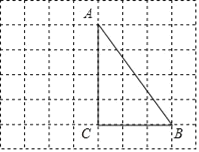
【题目】如图所示,在每个边长都为1的小正方形组成的网格中,点![]() 、
、![]() 、
、![]() 均为格点.
均为格点.
(1)线段![]() 的长度等于______;
的长度等于______;
(2)若![]() 为线段
为线段![]() 上的动点,以
上的动点,以![]() 、
、![]() 为邻边的四边形
为邻边的四边形![]() 为平行四边形,当
为平行四边形,当![]() 长度最小时,请你借助网格和无刻度的直尺画出该平行四边形,并简要说明你的作图方法:__________(不要求证明).
长度最小时,请你借助网格和无刻度的直尺画出该平行四边形,并简要说明你的作图方法:__________(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,O为坐标原点,A(1,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P的个数共有( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
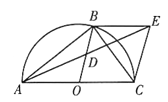
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 为
为![]() 上一点,且点
上一点,且点![]() 不与点
不与点![]() 重合,点
重合,点![]() 为半径
为半径![]() 的中点,过点
的中点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
(1)求证:点![]() 为
为![]() 的中点;
的中点;
(2)连接![]() ,若
,若![]() ,请直接写出
,请直接写出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有五张背面相同的卡片,正面分别印有圆、矩形、等边三角形、菱形、平行四边形(邻边不相等且不垂直),现将五张卡片正面朝下洗匀任意摆放,从中随机抽取两张,抽到的两张卡片上都恰好印的既是中心对称又是轴对称的图形的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com