【题目】如图，△ABC在坐标平面内三顶点的坐标分别为A（1，1）、B（3，3）、C（3，0）．
①根据题意，请你在图中画出△ABC；
②以B为位似中心，在如图的格子中画出一个与△ABC相似的△BA′C′，且△BA′C′与△ABC相似比是2：1，并分别写出顶点A′和C′的坐标．
科目：初中数学 来源： 题型：
【题目】如图：二次函数y＝ax2+bx+c的图象所示，下列结论中：①abc＞0；②2a+b＝0；③当m≠1时，a+b＞am2+bm；④a﹣b+c＞0；⑤若ax12+bx1＝ax22+bx2，且x1≠x2，则x1+x2＝2，正确的个数为（ ）
A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某市为了解旅游人数的变化情况，收集并整理了2017年1月至2019年12月期间的月接待旅游量（单位：万人次）的数据并绘制了统计图如下：
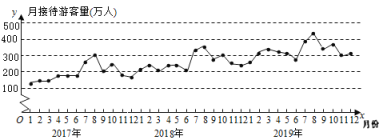
根据统计图提供的信息，下列推断不合理的是（ ）
A.2017年至2019年，年接待旅游量逐年增加
B.2017年至2019年，各年的月接待旅游量高峰期大致在7，8月份
C.2019年的月接待旅游量的平均值超过300万人次
D.2017年至2019年，各年下半年（7月至12月）的月接待旅游量相对于上半年（1月至6月）波动性更小，变化比较平稳
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在平面直角坐标系
中，抛物线
与
轴交于点
和点
，与
轴交于点
.
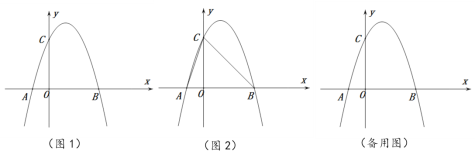
（1）求抛物线的表达式；
（2）如图2，连接
，点
是线段
上方抛物线上的一个动点，当
时，求点的坐标；
（3）在抛物线上是否存在点
，使得
？若存在，请求出点
的坐标，若不存在，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】把分别标有数字1，2，3，4的四个小球放入A袋内，把分别标有数字－1，－2，－2，－3，5的五个小球放入B袋内，所有的小球除了标有的数字不同外，其余完全相同.
（1）学生甲从A、B两个袋子中各摸出一个小球，求这两个小球上的数字互为相反数的概率.
（2）当B袋中标有5的小球的数字变为 时，（1）中的概率为
.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将△ABC绕点C顺时针旋转得到△DEC，使点A的对应点D恰好落在边AB上，点B的对应点为E，连接BE，下列四个结论：1. AC=AD 2. AB⊥EB 3.BC=EC 4.∠A=∠EBC其中一定正确的是( )
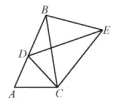
A.1 2B.2 3C.3 4D.2 3 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，抛物线y=a
-4ax与x轴交于A，B两点(A在B的左侧)．
(1)求点A，B的坐标；
(2)已知点C(2，1)，P(1，-
a)，点Q在直线PC上，且Q点的横坐标为4．
①求Q点的纵坐标（用含a的式子表示）；
②若抛物线与线段PQ恰有一个公共点，结合函数图象，求a的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，是二次函数
图象的一部分，对称轴是直线
，与
轴的交点是（0，3），则下列结论中正确的是（ ）
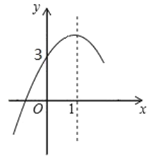
A.
；B.
>0；C.当0<
<2时，>3；D.关于的方程
有两个相等的实数根
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，点到直线的距离即为点到直线的垂线段的长．
（1）如图1，取点M（1，0），则点M到直线l：y＝
x﹣1的距离为多少？
（2）如图2，点P是反比例函数y＝
在第一象限上的一个点，过点P分别作PM⊥x轴，作PN⊥y轴，记P到直线MN的距离为d0，问是否存在点P，使d0＝
？若存在，求出点P的坐标，若不存在，请说明理由．
（3）如图3，若直线y＝kx+m与抛物线y＝x2﹣4x相交于x轴上方两点A、B（A在B的左边）．且∠AOB＝90°，求点P（2，0）到直线y＝kx+m的距离最大时，直线y＝kx+m的解析式．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
