
【题目】已知菱形的周长为20 cm,两对角线长度比为3:4,则对角线长分别为( )
A.12cm.16cmB.6cm,8cmC.3cm,4cmD.24cm,32cm
科目:初中数学 来源: 题型:
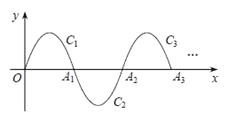
【题目】如图,在平面直角坐标系xOy中,已知抛物线(0≤x≤3)在x轴上方的部分,记作C1,它与x轴交于点O,A1,将C1绕点A1旋转180°得C2,C2与x 轴交于另一点A2.请继续操作并探究:将C2绕点A2旋转180°得C3,与x 轴交于另一点A3;将C3绕点A2旋转180°得C4,与x 轴交于另一点A4,这样依次得到x轴上的点A1,A2,A3,…,An,…,及抛物线C1,C2,…,Cn,….则点A4的坐标为 ;Cn的顶点坐标为 (n为正整数,用含n的代数式表示) .
查看答案和解析>>
科目:初中数学 来源: 题型:
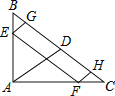
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=2,AC=3,D为BC的中点,动点E,F分别在AB,AC上,分别过点EG∥AD∥FH,交BC于点G、H,若EF∥BC,则EF+EG+FH的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一场足球比赛中,一球员从球门正前方10米处起脚射门,当球飞行的水平距离为6米时达到最高点,此时球高为3米.
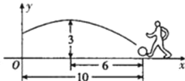
(1)如图建立直角坐标系,当球飞行的路线为一抛物线时,求此抛物线的解析式.
(2)已知球门高为2.44米,问此球能否射中球门(不计其它情况).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防“甲型H1N1”,某校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的含药量低于1.6mg时,生方可进教室,那么从消毒开始,至少需要几分钟后,生才能进入教室?
(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.
查看答案和解析>>
科目:初中数学 来源: 题型:
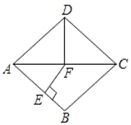
【题目】如图,在菱形ABCD中,∠BAD═70°,AB的垂直平分线交对角线AC于点F.垂足为E,连接DF,则∠CDF等于( )
A.60°B.65°C.70°D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】石狮泰禾某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“十一”国庆节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)设每件童装降价x元时,每天可销售______ 件,每件盈利______ 元;(用x的代数式表示)
(2)每件童装降价多少元时,平均每天赢利1200元.
(3)要想平均每天赢利2000元,可能吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”、“30元”的字样.规定:顾客在本超市一次性消费满200元,就可以在箱子里先后摸出两个小球(每一次摸出后不放回).某顾客刚好消费200元,则该顾客所获得购物券的金额超过30元的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com