
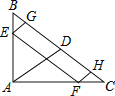
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=2,AC=3,D为BC的中点,动点E,F分别在AB,AC上,分别过点EG∥AD∥FH,交BC于点G、H,若EF∥BC,则EF+EG+FH的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
先根据勾股定理计算出BC=![]() ,再根据直角三角形斜边上的中线性质得到DA=DB=DC,则∠B=∠DAB,∠C=∠DAC,由于EF∥BC,EG∥AD∥FH,所以∠BEG=∠DAB,∠CFH=∠DAC,EF=GH,则∠B=∠BEG,∠C=∠CFH,根据等呀哦三角形的判定得BG=EG,FH=HC,所以EF+EG+FH=GH+BG+HC=BC=
,再根据直角三角形斜边上的中线性质得到DA=DB=DC,则∠B=∠DAB,∠C=∠DAC,由于EF∥BC,EG∥AD∥FH,所以∠BEG=∠DAB,∠CFH=∠DAC,EF=GH,则∠B=∠BEG,∠C=∠CFH,根据等呀哦三角形的判定得BG=EG,FH=HC,所以EF+EG+FH=GH+BG+HC=BC=![]() .
.
∵∠BAC=90°,AB=2,AC=3,
∴BC=![]() =
= ![]() ,
,
∵∠BAC=90°,D为BC的中点,
∴DA=DB=DC,
∴∠B=∠DAB,∠C=∠DAC,
∵EF∥BC,EG∥AD∥FH,
∴∠BEG=∠DAB,∠CFH=∠DAC,EF=GH,
∴∠B=∠BEG,∠C=∠CFH,
∴BG=EG,FH=HC,
∴EF+EG+FH=GH+BG+HC=BC=![]() .
.
故选B.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
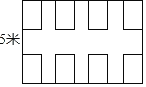
【题目】如图所示的是一个宽5米的餐厅,只能放8张餐桌.现计划扩建增加座位,只能对原宽度进行加长,设加长后的长度为m米.若餐厅的餐桌数为y,经计算,得到如下数据:(注:m和y都为正整数)
m(米) | 5 | 8 | 11 | 14 | …… |
餐桌数y(张) | 8 | 12 | 16 | …… |
(1)根据表中数据的规律,完成以上表格;
(2)求出y关于m的函数解析式;
(3)若这家餐厅至少要有80张餐桌,求m的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
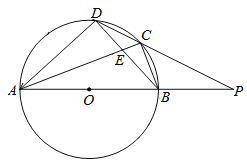
【题目】如图,在四边形ABCD中,以AB为直径的半圆O经过点C,D.AC与BD相交于点E,CD2=CE·CA,分别延长AB,DC相交于点P,PB=BO,CD=2![]() .则BO的长是_________.
.则BO的长是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是圆
是圆![]() 的直径,
的直径,![]() 是圆
是圆![]() 上一点,
上一点,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,交
,交![]() 的切线
的切线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
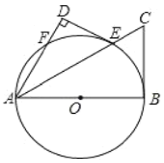
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,
,
①求![]() 的值;②若点
的值;②若点![]() 为
为![]() 上一点,求
上一点,求![]() 最小值.
最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学就“戏曲进校园”活动的喜爱情况进行了随机调查,对收集的信息进行了统计,绘制了下面两幅尚不完整的统计图.请你根据统计图所提供的信息解答下列问题:(图中![]() 表示“很喜欢”,
表示“很喜欢”,![]() 表示“喜欢”,
表示“喜欢”,![]() 表示“一般”,
表示“一般”,![]() 表示“不喜欢”)
表示“不喜欢”)
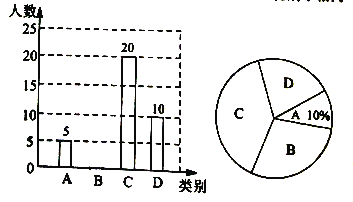
(1)被调查的总人数是_________,扇形统计图中![]() 部分所对应的扇形圆心角的度数为_________;
部分所对应的扇形圆心角的度数为_________;
(2)补全条形统计图;
(3)在抽取的![]() 类5人中,刚好有甲、乙、丙3个女生和丁、戊2个男生,从中随机抽取两个同学担任两角色,用画树状图或列表法求出抽到的两个学生性别不相同的概率.
类5人中,刚好有甲、乙、丙3个女生和丁、戊2个男生,从中随机抽取两个同学担任两角色,用画树状图或列表法求出抽到的两个学生性别不相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,是全国最大的瓷碗造型建筑,座落于江西景德镇,整体造型概念来自“宋代影青斗笠碗”,造型庄重典雅,象征“万瓷之母”.小敏为了计算该建筑物横断面(瓷碗橫断面ABCD为等腰梯形)的高度,如图2,她站在与瓷碗底部AB位于同一水平面的点P处测得瓷碗顶部点D的仰角为45°,而后沿着一段坡度为0.44(坡面与水平线夹角的正切值)的小坡PQ步行到点Q(此过程中AD,AP,PQ始终处于同一平面)后测得点D的仰角减少了5°.已知坡面PQ的水平距离为20米,小敏身高忽略不计,试计算该瓷碗建筑物的高度.(参考数据:sin 40°≈0.64,tan 40°≈0.84)
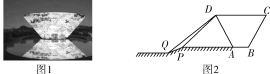
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 ,∠AFB=∠
(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ;
(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
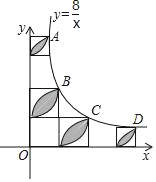
【题目】已知,A、B、C、D是反比例函数y=![]() (x>0)图象上四个整数点(横、纵坐标均为整数),分别过这些点向横轴或纵轴作垂线段,以垂线段所在的正方形(如图)的边长为半径作四分之一圆周的两条弧,组成四个橄榄形(阴影部分),则这四个橄榄形的面积总和是__________(用含π的代数式表示).
(x>0)图象上四个整数点(横、纵坐标均为整数),分别过这些点向横轴或纵轴作垂线段,以垂线段所在的正方形(如图)的边长为半径作四分之一圆周的两条弧,组成四个橄榄形(阴影部分),则这四个橄榄形的面积总和是__________(用含π的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com