
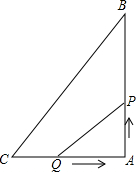
 如图,在△ABC中,∠BAC=90°,AB=4cm,AC=3cm,动点P、Q分别从点A、C同时出发,点P以2cm/s的速度向终点B移动,点Q以1cm/s的速度向终点A移动,当有一点到达终点时,另一点也停止运动,设运动的时间为t秒.
如图,在△ABC中,∠BAC=90°,AB=4cm,AC=3cm,动点P、Q分别从点A、C同时出发,点P以2cm/s的速度向终点B移动,点Q以1cm/s的速度向终点A移动,当有一点到达终点时,另一点也停止运动,设运动的时间为t秒.分析 (1)首先表示出AP和AQ的长,然后根据△APQ的面积为2cm2建立方程,求解即可;
(2)首先表示出AP和AQ的长,然后由勾股定理根据点P与Q的距离是4cm列出有关时间t的方程求解即可.
解答 解:(1)由题意,可得AP=2t,AQ=3-t,
∵△APQ的面积为2cm2,
∴$\frac{1}{2}$×2t×(3-t)=2,
解得t=1或2.
答:t为1或2时,△APQ的面积为2cm2;
(2)由题意,可得AP=2t,AQ=3-t,
∵点P与Q的距离是4cm,
∴(2t)2+(3-t)2=42,
解得:t=$\frac{3-2\sqrt{11}}{5}$或$\frac{3+2\sqrt{11}}{5}$,
∵t=$\frac{3-2\sqrt{11}}{5}$<0,不合题意舍去,
而0<t=$\frac{3+2\sqrt{11}}{5}$<2,符合题意.
答:t的值为$\frac{3+2\sqrt{11}}{5}$时点P与Q的距离是4cm.
点评 本题考查了一元二次方程的解法和应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:选择题
| A. | (x+2)(x+1)=x2 | B. | $\frac{1}{x^2}+\frac{1}{x}$-2=0 | C. | x2=5 | D. | x2+2x=x2-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com