
分析 (1)方程组利用代入消元法求出解即可;
(2)方程组利用加减消元法求出解即可.
(3)方程组利用加减消元法求出解即可;
(4)先把方程组中的方程化为不含分母及括号的方程,再用加减消元法求解即可.
解答 解:(1)$\left\{\begin{array}{l}{3x+4y=19①}\\{x-y=4②}\end{array}\right.$,
由②得:x=y+4,
代入①得:3y+12+4y=19,即y=1,
将y=1代入②得:x=5,
则方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{8y+5x=2①}\\{4y-3x=-10②}\end{array}\right.$,
①-②×2得:11x=22,即x=2,
将x=2代入①得:8y=-8,解得y=-1
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$.
(3)$\left\{\begin{array}{l}{x+2y=9①}\\{3x-2y=-1②}\end{array}\right.$
①+②得:4x=8,即x=2,
将x=2代入①得:2y=7,解得y=$\frac{7}{2}$,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=\frac{7}{2}}\end{array}\right.$.
(4))原方程组可化为$\left\{\begin{array}{l}{3x+4y=36①}\\{3x-2y=9②}\end{array}\right.$,
①-②得,6y=27,解得y=$\frac{9}{2}$,
把y=$\frac{9}{2}$代入②得,3x-9=9,解得x=6,
故此方程组的解为$\left\{\begin{array}{l}{x=6}\\{y=\frac{9}{2}}\end{array}\right.$.
点评 本题考查的是解二元一次方程组,熟知解二元一次方程组的加减消元法和代入消元法是解答此题的关键.


科目:初中数学 来源: 题型:解答题
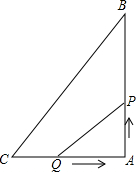 如图,在△ABC中,∠BAC=90°,AB=4cm,AC=3cm,动点P、Q分别从点A、C同时出发,点P以2cm/s的速度向终点B移动,点Q以1cm/s的速度向终点A移动,当有一点到达终点时,另一点也停止运动,设运动的时间为t秒.
如图,在△ABC中,∠BAC=90°,AB=4cm,AC=3cm,动点P、Q分别从点A、C同时出发,点P以2cm/s的速度向终点B移动,点Q以1cm/s的速度向终点A移动,当有一点到达终点时,另一点也停止运动,设运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 利用数轴解下列各题:
利用数轴解下列各题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com