
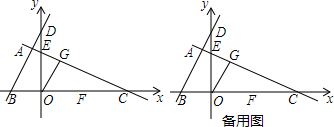
���� ��1�����ֱ��CE����ʽ���õ��߶�OE��OC��CE���ȣ��������������߶�OG��
��2�����÷ָ�����ı��ηָ��һ�������κ�һ�����Σ����������ɣ�
��3��ͨ���۲���Է���Q�����G�غϣ�ͨ��ֱ�������P���꼴�ɣ�
��� �⣺��1����$\frac{OE}{OC}=\frac{5}{12}��CE=\frac{169}{12}$��
��OE=5x��OC=12x��
�ࣨ5x��2+��12x��2=��$\frac{169}{12}$��2��
���x=$\frac{13}{12}$��
��OE=$\frac{65}{12}$��OC=$\frac{156}{12}$��
��OG��CE��G��
$\frac{1}{2}$��$\frac{65}{12}$��$\frac{156}{12}$=$\frac{1}{2}$��$\frac{169}{12}$��OG��
��ã�OG=$\frac{60}{12}$=5��
��OG�ij���Ϊ5��
��2����$\frac{OE}{OC}$=$\frac{5}{12}$��
��ֱ��CE����ʽΪ��y=-$\frac{5}{12}$x+b��
��OE=$\frac{65}{12}$��
��ֱ��CE����ʽΪ��y=-$\frac{5}{12}$x+$\frac{65}{12}$��
��ϵ�����飺$\left\{\begin{array}{l}{y=\frac{4}{3}x+\frac{25}{3}}\\{y=-\frac{5}{12}x+\frac{65}{12}}\end{array}\right.$��
��ã�x=-$\frac{35}{21}$��y=$\frac{55}{9}$��
��A��-$\frac{35}{21}$��$\frac{55}{9}$����
��ͼ������A��AH��x�ᣬ
��ֱ��AB�Ľ���ʽΪy=$\frac{4}{3}x+\frac{25}{3}$����x�ᡢy��ֱ��ڵ�B��D��
��B��-$\frac{25}{4}$��0����
��S�ı���ABOE=S��ABH+S����ABOE
=$\frac{1}{2}$��$\frac{25}{4}$-$\frac{35}{21}$����$\frac{55}{9}$+$\frac{1}{2}$��$\frac{55}{9}$+$\frac{65}{12}$����$\frac{35}{21}$
=$\frac{118}{5}$��
���ı���ABOE�����Ϊ$\frac{118}{5}$��
��3�����ڣ�
����Q��AC��ʱ��OG=OF=5��
�ߵ�Q��Ϊ��G��
���OPQ�ա�OPG��
��F��5��0����ֱ��CE����ʽΪ��y=-$\frac{5}{12}$x+$\frac{65}{12}$��
��P��5��$\frac{10}{3}$����
��OQ��AB��QΪ���㣬����QF����QF�Ĵ�ֱƽ���߽�AC��P��
��ʱ��OPQ�ա�OPF�����P��$\frac{65}{41}$��$\frac{195}{41}$����
����������P��5��$\frac{10}{3}$����P��$\frac{65}{41}$��$\frac{195}{41}$����
���� ��Ŀ������һ�κ����ۺ�Ӧ�ã�ͬʱ��Ŀ�������⡢ȫ�������ν��п��飬��Ŀ������ѣ���Ҫע���������ȷ�ԣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
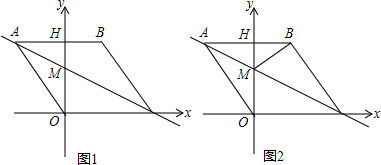
 ��ͼ����֪AD�ǡ�ABC�����Բ��ֱ����OΪԲ�ģ�AD=10cm��sinB=$\frac{4}{5}$����AC�ij�8��
��ͼ����֪AD�ǡ�ABC�����Բ��ֱ����OΪԲ�ģ�AD=10cm��sinB=$\frac{4}{5}$����AC�ij�8���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
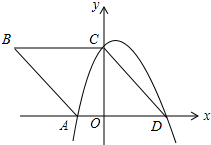 ��ͼ����ƽ��ֱ������ϵOxy�У��ı���ABCD�����Σ�����A��C��D�����������ϣ���AB=5��sinB=$\frac{4}{5}$��
��ͼ����ƽ��ֱ������ϵOxy�У��ı���ABCD�����Σ�����A��C��D�����������ϣ���AB=5��sinB=$\frac{4}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 �������ϱ�ʾa��b����ʵ���ĵ��λ����ͼ��ʾ����|a+b|-|a-b|�Ľ��Ϊ��������
�������ϱ�ʾa��b����ʵ���ĵ��λ����ͼ��ʾ����|a+b|-|a-b|�Ľ��Ϊ��������| A�� | 2a | B�� | 2b | C�� | 2a-2b | D�� | -2b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com