
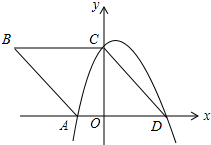
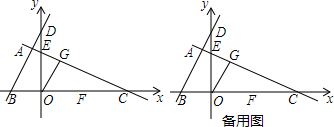
 如图,在平面直角坐标系Oxy中,四边形ABCD是菱形,顶点A、C、D均在坐标轴上,且AB=5,sinB=$\frac{4}{5}$.
如图,在平面直角坐标系Oxy中,四边形ABCD是菱形,顶点A、C、D均在坐标轴上,且AB=5,sinB=$\frac{4}{5}$.分析 (1)由菱形ABCD的边长和一角的正弦值,可求出OC.OD.OA的长,进而确定A.C.D三点坐标,通过待定系数法可求出抛物线的解析式.
(2)该题的关键点是确定点P的位置,△APE的面积最大,那么S△APE=$\frac{1}{2}$×AE×h中h的值最大,即点P离直线AE的距离最远,那么点P为与直线AB平行且与抛物线有且仅有的唯一交点.
(3)先待定过点F的直线,再求出解析式,根据直角三角形的勾股定理列方程,根据有且只有3个直角三角形得出△=0,求解即可.
解答 解:(1)∵四边形ABCD是菱形,
∴AB=AD=CD=BC=5,sinB=sinD=$\frac{4}{5}$;
Rt△OCD中,OC=CD•sinD=4,OD=3;
OA=AD-OD=2,即:
A(-2,0)、B(-5,4)、C(0,4)、D(3,0);
设抛物线的解析式为:y=a(x+2)(x-3),得:
2×(-3)a=4,a=-$\frac{2}{3}$;
∴抛物线:y=-$\frac{2}{3}$ x2+$\frac{2}{3}$ x+4.
(2)如图1,设直线AB:y1=kx+b,
把A(-2,0)、B(-5,4)坐标代入得
$\left\{\begin{array}{l}{0=-2k+b}\\{4=-5k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=-\frac{8}{3}}\end{array}\right.$,
∴AB:y1=-$\frac{4}{3}$ x-$\frac{8}{3}$;
∵S△APE=$\frac{1}{2}$AE•h,
∴当P到直线AB的距离最远时,S△ABC最大;
若设直线L∥AB,则直线L与抛物线有且只有一个交点时,该交点为点P;
设直线L:y=-$\frac{4}{3}$ x+m,当直线L与抛物线有且只有一个交点时,
-$\frac{4}{3}$x+m=-x2+x+4,且△=0;
求得:m=$\frac{11}{2}$,即直线L:y=-$\frac{4}{3}$ x+$\frac{11}{2}$;
解-$\frac{4}{3}$x+$\frac{11}{2}$=-x2+x+4得:x=$\frac{3}{2}$,
y=-$\frac{4}{3}$ x+$\frac{11}{2}$=$\frac{7}{2}$,
∴点P( $\frac{3}{2}$,$\frac{7}{2}$).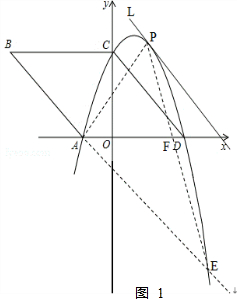
(3)
设过点F的直线解析式为:y=cx+d,
把点F(-6.0)代入得:
0=-6c+d,
d=6c,
∴y=cx+6c,
当∠AED=90°时,设点M(x,cx+6c)
可求AM2=(x+2)2+(cx+6c)2,
DM2=(x-3)2+(cx+6c)2
AD=3-(-2)=5,
根据题意
AM2+DM2=AD2,
∴(x+2)2+(cx+6c)2+(x-3)2+(cx+6c)2=52,
整理得:(c2+1)x2+(12c2-1)x+36c2-8=0,
由题意知:△=0,
解得:c=±$\sqrt{\frac{33}{136}}$,
所以满足条件的直线为:y=$\sqrt{\frac{33}{136}}$x+6$\sqrt{\frac{33}{136}}$,或y=-$\sqrt{\frac{33}{136}}$x-6$\sqrt{\frac{33}{136}}$,
把c=±$\sqrt{\frac{33}{136}}$代入::(c2+1)x2+(12c2-1)x+36c2-8=0,解得:x=-$\frac{10}{13}$,
此时y=±$\frac{68}{13}$$\sqrt{\frac{33}{136}}$
此时满足条件的点:M5(-$\frac{10}{13}$,$\frac{68}{13}$$\sqrt{\frac{33}{136}}$),M2(-$\frac{10}{13}$,-$\frac{68}{13}$$\sqrt{\frac{33}{136}}$)
当x=-2时,y=±4$\sqrt{\frac{33}{136}}$,当x=3时,y=±9$\sqrt{\frac{33}{136}}$,
所以点M1(-2,-4$\sqrt{\frac{33}{136}}$),M4(-2,4$\sqrt{\frac{33}{136}}$),M6(3,9$\sqrt{\frac{33}{136}}$),M3(3,-9$\sqrt{\frac{33}{136}}$),
综上所述当直线为:y=$\sqrt{\frac{33}{136}}$x+6$\sqrt{\frac{33}{136}}$时,有:M5(-$\frac{10}{13}$,$\frac{68}{13}$$\sqrt{\frac{33}{136}}$),M4(-2,4$\sqrt{\frac{33}{136}}$),M6(3,-9$\sqrt{\frac{33}{136}}$).
当直线为:y=-$\sqrt{\frac{33}{136}}$x-6$\sqrt{\frac{33}{136}}$时,有:M1(-2,-4$\sqrt{\frac{33}{136}}$),M2(-$\frac{10}{13}$,-$\frac{68}{13}$$\sqrt{\frac{33}{136}}$),M3(3,-9$\sqrt{\frac{33}{136}}$).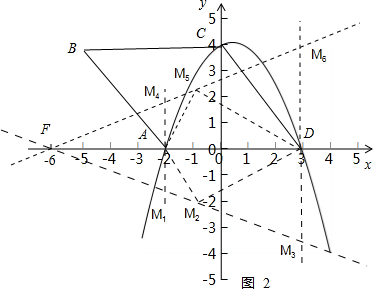
点评 此题主要考察菱形性质在坐标系中的应用,三角形面积的最大问题,和点的存在性问题,难度很大,熟练掌握相关性质,并注意分类讨论思想是解题的关键.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
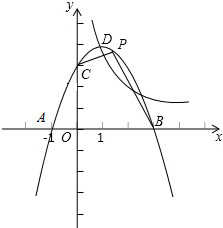 如图,抛物线y=ax2+bx+3与x轴交于A、B两点(A在B的左边),与y轴交于C,tan∠CAB=3;双曲线$y=\frac{k}{x}$(k≠0)经过抛物线y=ax2+bx+3的顶点,点D的横坐标为1.
如图,抛物线y=ax2+bx+3与x轴交于A、B两点(A在B的左边),与y轴交于C,tan∠CAB=3;双曲线$y=\frac{k}{x}$(k≠0)经过抛物线y=ax2+bx+3的顶点,点D的横坐标为1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 利用数轴解下列各题:
利用数轴解下列各题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com