
某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
| A型利润 | B型利润 | |
| 甲店 | 200 | 170 |
| 乙店 | 160 | 150 |
(1)设分配给甲店A型产品x件,这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并求出x的取值范围;
(2)若要求总利润不低于17560元,有多少种不同分配方案,并将各种方案设计出来;
(3)为了促销,公司决定仅对甲店A型产品让利销售,每件让利a元,但让利后A型产品的每件利润仍高于甲店B型产品的每件利润.甲店的B型产品以及乙店的A,B型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
解:依题意,分配给甲店A型产品x件,则甲店B型产品有(70-x)件,乙店A型有(40-x)件,B型有{30-(40-x)}件,则
(1)W=200x+170(70-x)+160(40-x)+150(x-10)=20x+16800.
由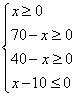 ,解得10≤x≤40.
,解得10≤x≤40.
(2)由W=20x+16800≥17560,∴x≥38.
∴38≤x≤40,x=38,39,40.
∴有三种不同的分配方案.
方案一:x=38时,甲店A型38件,B型32件,乙店A型2件,B型28件;
方案二:x=39时,甲店A型39件,B型31件,乙店A型1件,B型29件;
方案三:x=40时,甲店A型40件,B型30件,乙店A型0件,B型30件.
(3)依题意:200-a>170,即a<30,
W=(200-a)x+170(70-x)+160(40-x)+150(x-10)=(20-a)x+16800,
(10≤x≤40).
①当0<a<20时,20-a>0,W随x增大而增大,∴x=40,W有最大值,即甲店A型40件,B型30件,乙店A型0件,B型30件,能使总利润达到最大;
②当a=20时,10≤x≤40,W=16800,符合题意的各种方案,使总利润都一样;
③当20<a<30时,20-a<0,W随x增大而减小,∴x=10,W有最大值,即甲店A型10件,B型60件,乙店A型30件,B型0件,能使总利润达到最大.


科目:初中数学 来源: 题型:
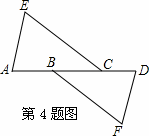
如图,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加下列选项中的……( )
A.AB=CD; B.EC=BF; C.∠A=∠D; D.AB=BC;
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
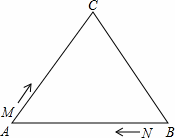
如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.
(1)点M、N运动几秒后,M、N两点重合?
(2)点M、N运动几秒后,可得到等边三角形△AMN?
(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形?如存在,请求出此时M、N运动的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com